Table of Contents
EPGY - Day 3
Morning
Question of the Day: You have two eggs and a 100 story building! You are told to find the highest floor that you can safely drop the eggs from without them breaking. These eggs could be pretty strong, so it is possible that they will not break even after being dropped from the very highest floor. Come up with a strategy to minimize the number of times you need to drop the eggs to discover the desired floor. One strategy is to drop an egg from the first floor, second floor, third floor, and so on until that egg breaks. This could require up to 100 egg drops though! A better strategy would be to start by dropping an egg from the 51th floor. If that egg breaks, then switching to our old strategy will take at most 50 drops. If the egg doesn’t break, then we can keep working our way up the floors. This strategy guarantees at most 50 drops. How much better can you do?
- House Keeping
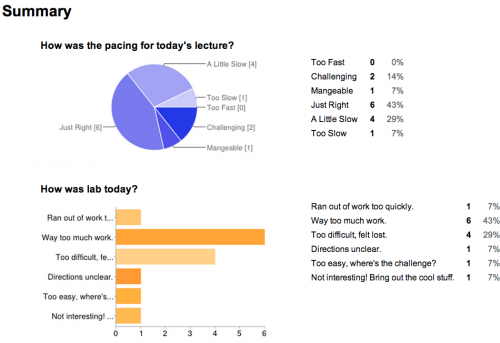
- Poll Results
- “Your value is not determined by how hard or easy something is.”
- Google Group
- Syllabus is updated!
- Transition from Believability: Turing Test Papers
- AI Communities/Culture
- Recursion
- Factorial
-
- Discussion: Imperative vs Declarative (Functional)
Declarative: Logic
% Towers of Hanoi via Logic Progamming peg(a;b;c). disk(1..4). init_on(1..4,a). goal_on(1..4,c). moves(15). % Generate 1 { move(D,P,T) : disk(D) : peg(P) } 1 :- moves(M), T = 1..M. % Define move(D,T) :- move(D,_,T). on(D,P,0) :- init_on(D,P). on(D,P,T) :- move(D,P,T). on(D,P,T+1) :- on(D,P,T), not move(D,T+1), not moves(T). blocked(D-1,P,T+1) :- on(D,P,T), disk(D), not moves(T). blocked(D-1,P,T) :- blocked(D,P,T), disk(D). % Test :- move(D,P,T), blocked(D-1,P,T). :- move(D,T), on(D,P,T-1), blocked(D,P,T). :- goal_on(D,P), not on(D,P,M), moves(M). :- not 1 { on(D,P,T) : peg(P) } 1, disk(D), moves(M), T = 1..M. #hide. #show move/3.
Declarative: Functional
;;; -*- Mode: LISP; Syntax: Common-lisp; ;;; http://www.apl.jhu.edu/~hall/lisp/Hanoi.lisp ;;;========================================================================= ;;; Simple towers of Hanoi program. Note that Start-Peg and Goal-Peg are ;;; integers from 1 to 3 indicating the peg number. Ie to move 4 discs, ;;; starting on the first peg and finishing on the last one, execute ;;; (Towers 4 1 3) ;;; ;;; 1992 Marty Hall. hall@aplcenmp.apl.jhu.edu (defun Towers (Number-of-Discs Start-Peg Goal-Peg) (cond ((= 1 Number-of-Discs) (format t "~%Move Top Disc from peg ~D to peg ~D." Start-Peg Goal-Peg)) (t (Towers (1- Number-of-Discs) Start-Peg (Remaining-Peg Start-Peg Goal-Peg)) (Towers 1 Start-Peg Goal-Peg) (Towers (1- Number-of-Discs) (Remaining-Peg Start-Peg Goal-Peg) Goal-Peg)))) ;;;========================================================================= ;;; Given two peg numbers, what is the peg number of the third peg? (defun Remaining-Peg (Peg1 Peg2) (- 6 Peg1 Peg2))
- Reviewing Code: Style, Approaches, Concepts
- Pass by Value vs Pass by Reference (Primitives and Objects)
- Briefly touch on Android (SDK, ADT, AVD)
- Debugging
-
- Array
- List
- Stack - Good for “Undo”
- Queue - does not use “push” and “pop”
- Algorithms
- Search
- Divide and Conquer!
- Sort
Afternoon
Disclaimer: Not everyone filled out the form. Also, this isn't a measure of anyone's merit, it's just to get a sense of where things are in the class. “Easy” and “Hard” are very relative terms.