Motivations and Needs for Scientific Computing¶
Let’s begin our first class with a couple of interesting scenarios.
Scenario 1¶
Consider you’re a chief scientist in a big aerospace research lab. See Figure 1. You’re given a mission to develop a new aerospace plane that can reach at hypersonic speed (> Mach 5) within minutes after taking off. Its powerful supersonic combustion ramjets continue to propel the aircraft even faster to reach to a velocity near 26,000 ft/s (or 7.92 km/s, or Mach 25.4 in air at high altitudes, or a speed of NY to LA in 10 min), which is simply a low Earth orbital speed. This is the concept of transatmospheric vehicle the subject of study in several countries during the 1980s and 1990s. When designing such extreme hypersonic vehicles, it is very important to understand full three-dimensional flow field over the vehicle with great accuracy and reliability. Unfortunately, ground test facilities – wind tunnels – do not exist in all the flight regimes around such hypersonic flight. We neither have no wind tunnels that can simultaneously simulate the higher Mach numbers and high flow field temperatures to be encountered by transatmospheric vehicles.

Figure 1: DARPA’s Falcon HTV-2 unmanned aircraft can max out at a speed of about 16,700 miles per hour – Mach 22, NY to LA in 12.
Scenario 2¶
Consider you’re a theoretical astrophysicist who tries to understand core collapse supernova explosions. See Figure 2. The theory tells us that very massive starts can undergo core collapse when the core fail to sustain against its own gravity due to unstable behavior of nuclear fusion. We simply cannot find any ground facilities that allow us to conduct any laboratory experiments in such highly extreme energetic astrophysical conditions. It is also true that in many astrophysical circumstances, both temporal and spatial scales are too huge to be operated in laboratory environments.
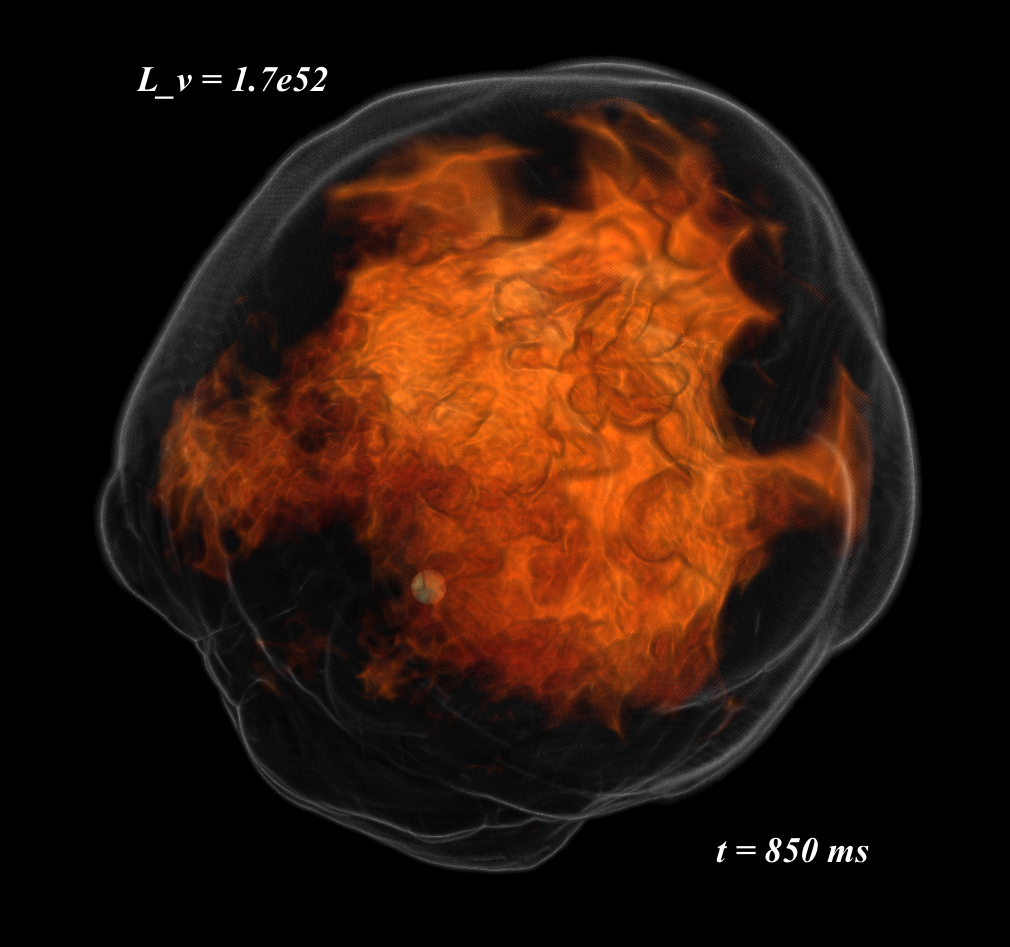
Figure 2: FLASH simulations of neutrino-driven core-collapse supernova explosions. Sean Couch (2013), ApJ, 775, 35.
Scenario 3¶
Consider you a golf ball manufacturer. See Figure 3. Your goal is to understand flow behaviors over a flying golf ball in order to make a better golf ball design (and become a millionaire!) Although you’ve already collected a wide range of the laboratory experimental data on a set of golf ball shapes (i.e., surface dimple design), you realize that it is very hard to analyze the data and understand them because the data are all nonlinearly coupled and can’t be isolated easily. To keep your study in a better organized way, you wish to perform a set of parameter studies by controlling flow properties one by one so that you can also make reliable flow prediction for a new golf ball design.

Figure 3: Contours of azimuthal velocity over a golf ball: (a) Re = 2.5 x 10^4; (b) Re = 1.1 x 10^5. C. E. Smith et al. (2010), Int. J. Heat and Fluid Flow, 31, 262-273.
As briefly hinted above, in practice there are various levels of difficulties encountered in real experimental setups. When performing the above mentioned research work, computational fluid dynamics (CFD) therefore can be the major player that leads you to success because you obtain mathematical controls in numerical simulations. Let us take an example how numerical experiment via CFD can elucidate physical aspects of a real flow field. Consider the subsonic compressible flow over an airfoil. We are interested in answering the differences between laminar and turbulent flow over the airfoil for Re = 10^5. For the computer program (assuming the computer algorithm is already well established, validated and verified!), this is a straightforward matter – it is just a problem of making one run with the turbulence model switched off (for the laminar setup), another run with the turbulence model switched on (for the turbulent flow), followed by a comparison study of the two simulation results. In this way one can mimic Mother Nature with simple knobs in the computer program – something you cannot achieve quite readily (if at all) in the wind tunnel. Without doubt, however, in order to achieve such success using CFD, you’d better to know what you do exactly when it comes to numerical modeling.
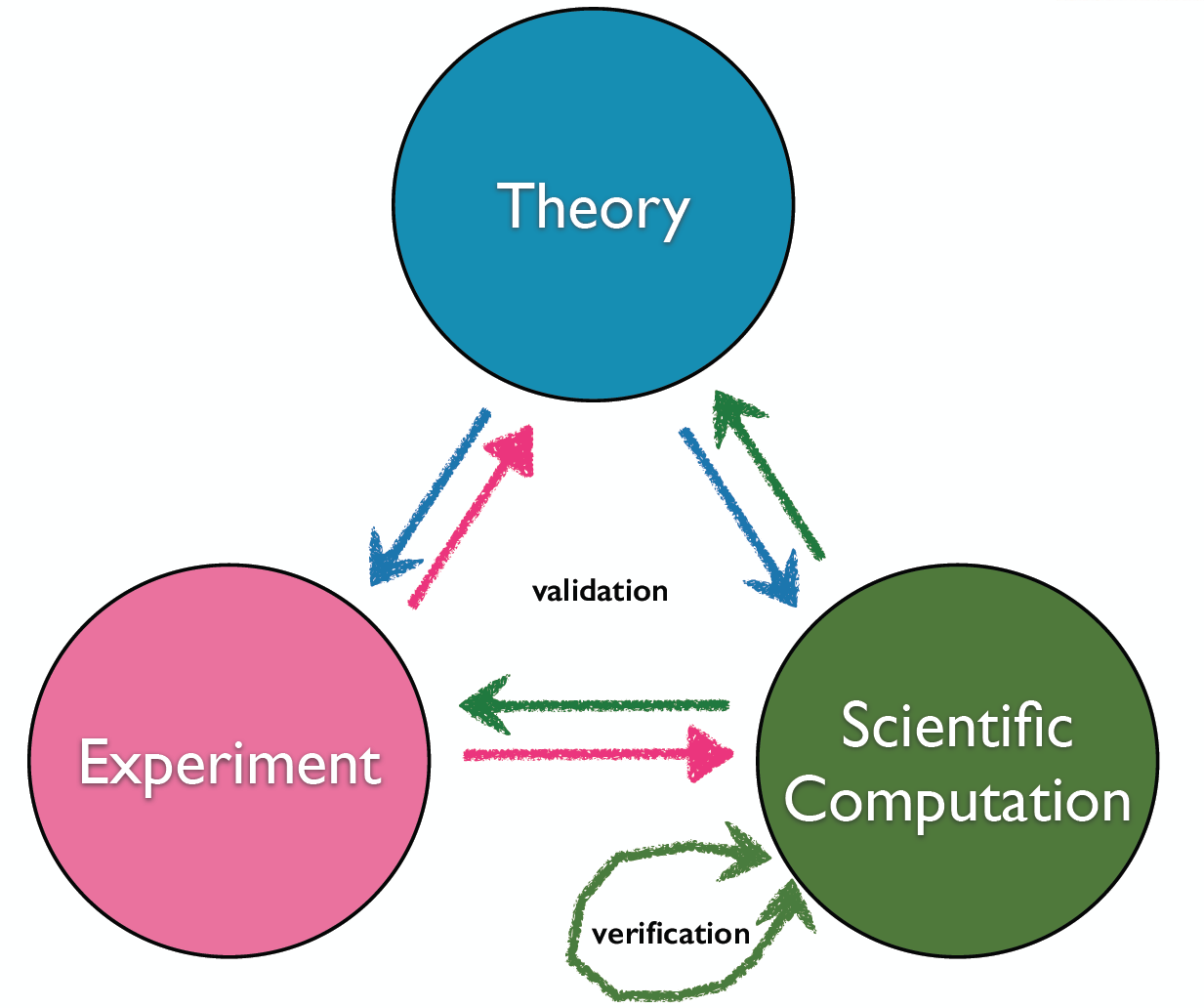
Scientific computation as a Third Scientific Tool¶
We are now ready to define what scientific computing is. It is a scientific tool, similar to experimental tools, used to gain greater physical insights into problems of interest. It involves a study of solving of ODEs and PDEs numerically on a discretized system that, given the available computer resources, best approximates the real geometry and fluid flow phenomena of interests. Modern scientific computing constitutes a new “third approach” in studying and developing the whole discipline of various areas in modern science. See Figure 4.
For example, the real-world applications of computational fluid dynamics (CFD) are one of the most active areas in science that fully utilize scientific computing. Scientists try to apply CFD to real problems that do not have known analytical solutions, in which CFD plays a key role as a scientific vehicle to solve flow problems that cannot be solved in any other way.
The similar philosophy applies to various different areas of physical sciences as well, including social sciences, engineerings, etc. where computation plays a key important role to provide a reliable tool for predictive sciences.
The main goal in this class is to collect our knowledges to better understand how and what computational tools to use, i.e., softwares and hardwares. And you are all welcome on board!