Table of Contents
Assignment 8
Don't forget to cyber stalk tomorrow's skype guests and leave feedback before the end of the day!
Lab 0 - Wrapping up!
- Clean up your EPGY Projects
- Clean up your blog and make sure all your projects are posted with Photos
- E-Mail Tracy and Dave thanking them for their lightening skype
Lab 1 - EPGYkNN
Review this here:
http://www.eecs.qmul.ac.uk/~christof/html/courses/ml4dm/week04-knn-naivebayes-4pp.pdf
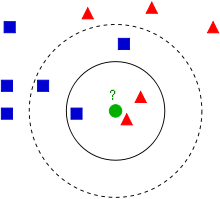
You may recall that I mentioned that lazy learning is when we take a training set and do nothing to build our model. The best example of a classifier that uses this approach is k-Nearest Neighbors (kNN). In kNN, we classify a testing example by finding the k most similar training examples, then allowing these training examples to “vote” on the label for the testing example. For example:
In this example (thanks wikipedia!) our classification task has two labels, blue and red, and want to classify the green circle from the test set as either blue or red. Using 3NN, we see that of the three nearest neighbors, the red examples dominate, so the circle would be labeled red. In 5NN, however, the three blue examples dominate the five nearest neighbors, so the circle is labeled blue.
The value of k that we choose has a huge impact on the performance of our classifier. As k approaches the size of the training set, we will classify based on which label is more common. Also large values of k. If k is one, then we are subject to problems with noise in our data set. Also note also that we use odd values of k so as to avoid ties in the case of binary classification.
So far I have not left you with a notion of distance or similarity. This is a difficult problem which goes hand in hand with the problem of choosing features to begin with. When representing data in feature space, we have to carefully select our distance measure to make sure no features have bias due to their range. For now, it is fine to think of the distance between points as Euclidean distance:
Your task will be to implement this algorithm. Download the starter code here. Import the project and read over the code that is already living there. There are two places you need to need to edit the starter code:
- Datum.distanceTo() – Every datum should be able to calculate the distance to another Datum
- KNNClassifier.classify() – This will be the bulk of the work. You need to classify each Datum, then report on how well you perform on the full test set.
Once you have a functioning program, try testing it on different (odd) values of k, thinking about the complexity of the process. Submit your code along with your results in the comments.
(Deliverable) The following are some questions to think about; discuss in a blog post about kNN (with photos):
- This classification problem is not obviously doable with Naive Bayes. How could you use a Naive Bayes classifier to perform classification on the given data set? How well will it perform?
- In general, on what data sets will kNN perform well?
- I included a higher dimensional data set for you to use. Try testing your classifier with it. What are your results? How do you think the higher dimensionality affects kNN?
- In general, on what data sets will it perform poorly?
- Which classifier do you prefer, Naive Bayes or kNN?
Lab 2 - EPGYkNNVisual
https://dl.dropboxusercontent.com/u/3235343/Games/kdteapot.pdf
Above is the description I used to build my kNN visualizer. I made mine a sideways ASCII binary tree. You can also see some spacial visualizations in the screenshots of my paper. You can choose how you'd like to visualize your datastructure. Using a Binary Tree or kD-Tree is only ONE WAY to classify data.
Here's the ACMStarter if you'd like to create it with a graphics package:
http://www.stanford.edu/~bholtz/AIClass/ExampleCode/ACMGraphics.zip
Here's a Binary Tree interface for Java:
http://docs.oracle.com/javase/6/docs/jdk/api/javac/tree/com/sun/source/tree/BinaryTree.html
(Deliverable) Add your visualizations to the kNN post, if you've done it already. Otherwise, write a post about kNN with a screen shot of your visualization and answer the questions above.
Note: Your visualization program must successfully classify the data points, and use some kind of visual representation to illustrate that your program is indeed creating an optimization.
You have two options:
- Create a visualization with the data points given in Lab 1
- Redo the visualization that was done in my paper with as many random points as you need to make your visualization convincing
(option 2 is easier)
Lab 3
Let’s work through an example of classification using a Binary Naive Bayes Classifier. If you want to code this up, feel free, but it is probably easier to just use pen and paper. We are not going to look over your answers, so just check them against your neighbors’. Here goes:
You land on an alien planet and want to categorize the local fauna, but you have trouble telling apart two similar looking species of space slugs. A friendly alien, whose life has been spent telling the A-type and B-type space slugs apart, comes to your aid, and shows some good characteristic traits of the slugs that you can use to identify them, then he separates a group of 30 space slugs into A-type and B-type slugs. In order to classify space slugs on your own, you build a Naive Bayes Classifier.
Space slugs all can have fluffy tails or non-fluffy tails, green ears or black ears, spots or no spots, and an extra tongue or no extra tongue. In order to convert each slug into features, I will represent each of the 30 slugs by 5 bits:
- if type-A, 0 if type-B
- if fluffy tail, 0 if not fluffy tail
- if green ears, 0 if black ears
- if spots, 0 if no spots
- if extra tongue, 0 if no extra tongue
So for example, a type-B space slug with a fluffy tail, black ears, no spots, and an extra tongue will be 01001. Here are the space slugs that your alien friend collected and tagged for you:
00010 01001 01000 00011 00000 01010 00000 00001 01001 01000 01000 01100 00000 00010 01111 11000 10011 11000 11000 10011 10000 11100 11000 11011 11000 00001 11000 00011 11111 01001
Use the first 5 rows to train your model, then test on the last row. Remember that a Naive Bayes Classifier assigns a label as follows:
- Priors (the probabilities that you model from your data) are computed from the training data: you need to model P(type-A slug) and P(type-B slug) as well as P(fluffy tail | type-A), P(no extra tongue | type-B), etc
- For example, P(black ears | type-B) = 9/10
- Compute P(type-A | observations) and P(type-B|observations) for each training example.
- Recall that we make the naive bayes assumption P(X1,X2,X3,…,Xn|type) = P(X1|type)…P(Xn|type)
- P(type-A | observations) is approximated by P(observation1|type-A) x … x P(observation4|type-A)
- Choose the more likely label!
Report how well your classifier performs. Is it a good classifier? How could we improve upon it? Do you notice any of the features that are more useful than others?
Imagine that we added another feature, has antennae, but this trait is incredibly rare in the type-A slug population. It is so rare, in fact, that we have no examples of it in our training set. This causes the computed value of our prior P(has antennae|type-A) to be 0, meaning we will never ever assign an example with an antennae to type-A! In order to combat this problem, we use smoothing. Smoothing is slightly modifying our data so that it is less noisy and hopefully closer to the underlying “true” model.
A simple type of smoothing is Laplace smoothing, or add-one smoothing, in which we simply pretend to have seen more examples of all possible types of observation. Now, rather than modeling P(extra tongue | type-A) = (# type-A with extra tongue) / (# type-A), we model P(extra tongue | type-A) = (# type-A with extra tongue + 1) / (# type-A + 2).
- Verify that the smoothing does not break the axioms of probability (i.e. P(extra tongue|type-A) + P(no extra tongue|type-A) = 1)
- Using, the Laplace smoothing, recalculate your model and report how well your classifier performs.
- Did smoothing improve your results? Why or why not?
- With what kind of data is Laplace smoothing helpful? When can you imagine it being harmful or helpful?