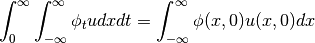Homework 2 (Due 6 pm, Wed, 2/15/2017)

Please submit your homework to your git repo by 6 pm, Wednesday, 2/15/2017.

Hints for Problem 4 in Homework 2

Using the definition of weak solutions, we want to show:

\int_0^\infty \int_{-\infty}^{\infty} [\phi_t u + \phi_x f(u)] dxdt = -\int_{-\infty}^{\infty} \phi(x,0) u(x,0) dx.

To show this, prove the following claims in steps:

Claim 1 - Show the first term in the definition is the right hand side:

\begin{equation} \int_0^\infty \int_{-\infty}^{\infty} \phi_t u dx dt = \int_{-\infty}^{\infty} \phi(x,0) u(x,0) dx \nonumber \end{equation}

Claim 1a - To prove Claim 1, you need to first prove:

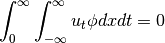
\begin{equation} \int_0^\infty \int_{-\infty}^{\infty} u_t \phi dx dt = 0 \nonumber \end{equation}

Claim 1b - To complete Claim 1, observe that:

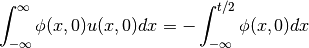
\begin{equation} \int_{-\infty}^{\infty} \phi(x,0) u(x,0) dx = - \int_{-\infty}^{t/2} \phi(x,0)dx \nonumber \end{equation}

Claim 2 - Show the second term in the definition is zero:

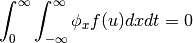
\begin{equation} \int_0^\infty \int_{-\infty}^{\infty} \phi_x f(u) dx dt = 0 \nonumber \end{equation}

Claim 2a - To prove Claim 2, you need to prove also:

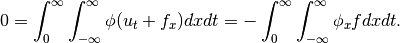
\begin{equation} 0 = \int_0^\infty \int_{-\infty}^{\infty} \phi (u_t + f_x) dx dt = -\int_0^\infty \int_{-\infty}^{\infty} \phi_x f dx dt. \nonumber \end{equation}

In the above, split the spatial integral into two parts and use the definition of 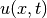u(x,t):

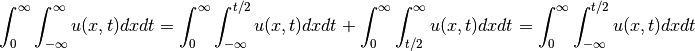
\int_0^{\infty}\int_{-\infty}^{\infty} u(x,t) dx dt = \int_0^{\infty}\int_{-\infty}^{t/2} u(x,t) dx dt + \int_0^{\infty}\int_{t/2}^{\infty} u(x,t) dx dt = \int_0^{\infty}\int_{-\infty}^{t/2} u(x,t) dx dt

and also use the fact that 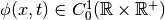\phi (x,t) \in C^1_0(\mathbb{R}\times \mathbb{R}^+).