Research Interests
My main research interests are in fluid dynamics and magnetohydrodynamics applied to astrophysics and occasionally geophysics. I specialize in semi-analytical work, using a combination of "pen-and-paper" calculations with moderate-size numerical computations. I also collaborate with researchers specialized in high-performance computing of fluid dynamical phenomena and help in the interpretation of the numerical results. My main research projects at the moment are:
- Large-scale magnetohydrodynamics of the solar interior
- Understanding the properties of fingering convection, with applications to oceanography and astrophysics
- Understanding the properties of double-diffusive convection, with applications to astrophysics
Projects I am still interested in but no longer actively working on for now are:
- Modeling turbulent convection
- Evolution of magnetized stars
- Modeling the dynamics of dust particles in proto-stellar disks
- The role of gyroscopic pumping in stellar interiors
My group has also developed efficient but easy-to-use parallel numerical algorithms for the solution of large block-tridiagonal systems, and for 2-point boundary-value problems.
Potential research projects are indicated in each section.
For a complete list of publications, see my Publications page.
Large-scale magnetohydrodynamics of the solar interior
Collaborators: Nic Brummell (UCSC Applied Mathematics), Douglas Gough (Institute of Astronomy, DAMTP), Cambridge, Lydia Korre (CU Boulder), Celine Guervilly (U. Newcastle)
Funding: NST MRI-0521566, NSF AST-0607495, NSF CAREER-0847477
The images below show, on the left, state-of-the-art helioseismic observations of the rotation profile of the Sun, and on the right, the current paradigm used to explain these observations (Gough & McIntyre, 1998).
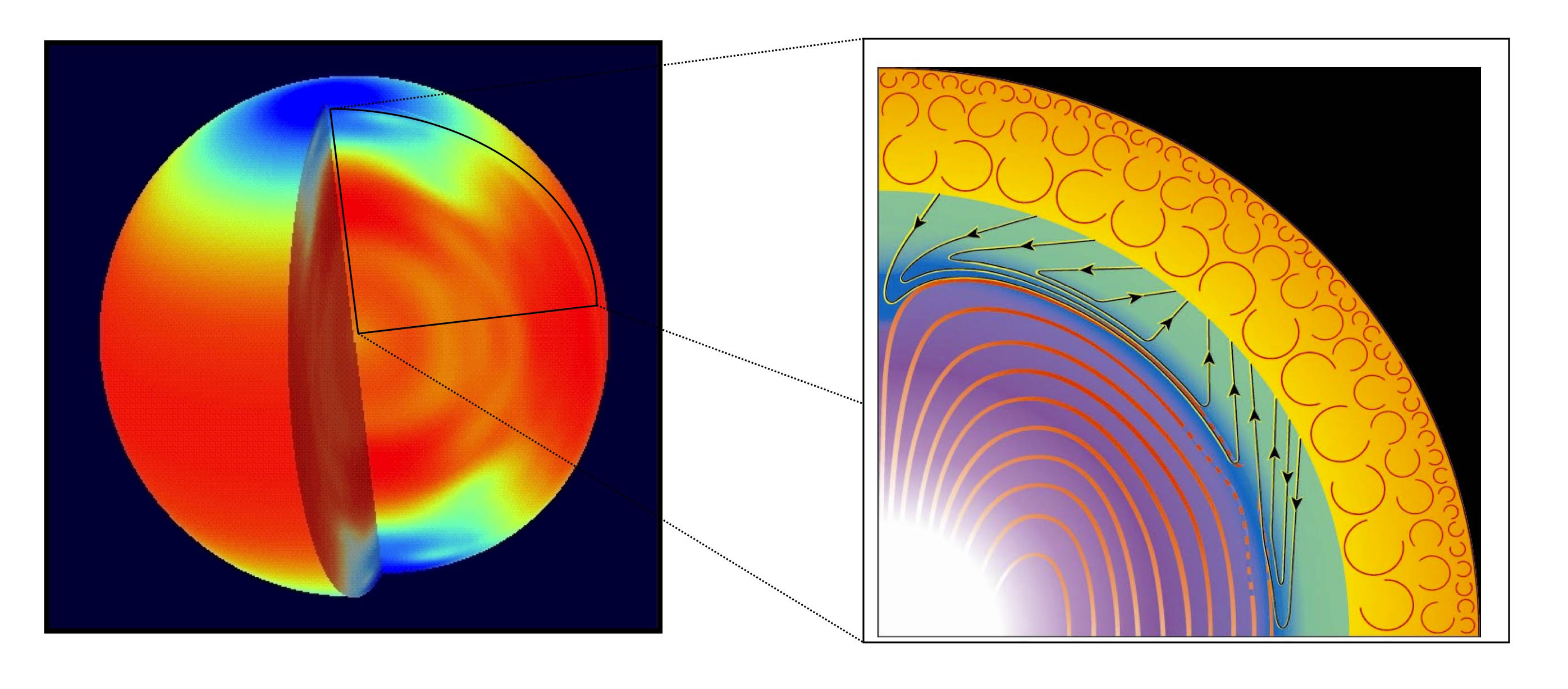
As shown on the left, the rotation profile of the Sun has three peculiarities. First, the outer regions are strongly differentially rotating, to the extent that fluid in the equator rotates around the polar axis in about 25 days, while fluid around the polar regions takes more than 30 days. Secondly, fluid in the interior is in near-uniform rotation. The transition between these two dynamically very distinct regions occurs precisely at the base of the solar convection zone, and is called "the solar tachocline". The third peculiarity is that the tachocline is extremely thin, with a thickness no larger than a few percent of the solar radius.
Why the Sun has such a peculiar rotation profile remains one of the longest-standing puzzles in solar physics. It is a crucial problem, however, since it is closely related to the origin of the solar magnetic cycle.
The most commonly invoked theory of the tachocline is depicted on the right-side figure. A large-scale magnetic field is thought to be embedded in the solar radiative interior, and holds the fluid in a state of rigid rotation via Ferraro's isorotation law. The magnetic field is prevented from diffusing into the convection zone by large-scale meridional flows, which are gyroscopically pumped by the convection and downwell into the interior.
In the past 20 years, I have devoted part of my research to the study of the solar tachocline along the line of thoughts described above.
With my collaborators, we have created a two-dimensional MHD code which finds steady-state solutions of the MHD equations in a spherical shell representing the stellar (or solar) interior (see Garaud & Garaud 2008). The code takes as input any reasonably smooth background stellar model, uses an artificial forcing term to model the differential rotation in the convective regions, and assumes the existence of a primordial "current" to maintain a large-scale primordial magnetic field. The code outputs the resulting total magnetic field, large-scale flows (meridional and azimuthal) and thermodynamical perturbations in the stellar interior.
Thanks to this code, we have established:
- The fundamental role of downwelling flows in the dynamics of the tachocline (Garaud & Brummell 2008, Garaud & Garaud 2008), as opposed to baroclinically-generated flows.
- Scaling laws for the amplitude of gyroscopically pumped flows as a function of the fluid parameters and global dynamics of the radiative interior (Garaud & Acevedo-Arreguin, 2009 and McCaslin, Garaud & Wood 2011, in prep.).
- How the rotation rate of the radiative interior depends on the dynamics of the tachocline region (Garaud & Guervilly, 2009).
Using the PARODY code, we are now proceeding to run numerical simulations of the entire solar interior along the model described above, to see if we can reproduce and explain the observed rotation pattern. In that case of course everything is more complex, since the nonlinear dynamics of turbulent convection must be accounted for. This has led so far to the publication of two papers by Lydia Korre, looking into:
- The impact of convection on the stratification of the solar interior (Korre et al. 2017)
- The dynamics of overshooting convection in a hydrodynamic Sun (ignoring magnetic fields) (Korre et al. 2019)
Potential PhD project: To be defined after discussions with collaborators.
Understanding the properties of fingering convection, with applications to oceanography and astrophysics
Collaborators: Nic Brummell (UCSC Applied Mathematics and Statistics), Timour Radko (NPS Monterey), Stephan Stellmach (U. Muenster, Germany), Toby Wood (UCSC Applied Mathematics and Statistics).
Funding: NSF FLUIDS-0933759
When the density of a fluid depends on (at least) two components, stably-stratified systems can undergo double-diffusive instabilities, leading to strong turbulent mixing. Two cases exist: the "fingering” instability, which often occurs in fluids which are thermally stably stratified, but have an inhomogeneous (destabilizing) composition and the "diffusive" instability, where the fluid is stably stratified despite an unstable thermal gradient. The latter is studied in the next section.
The most well-know example of the fingering instability occurs in the upper ocean (thermocline) in low and mid-latitudes, where heating and evaporation leads to warm salty water overlying cold and fresh
water. Since heat diffuses much faster than salt, fluid displaced downward rapidly loses its heat excess while maintaining its larger salt concentration. It becomes denser than the environment and continues to sink, forming structures called “salt-fingers", see the figure below.
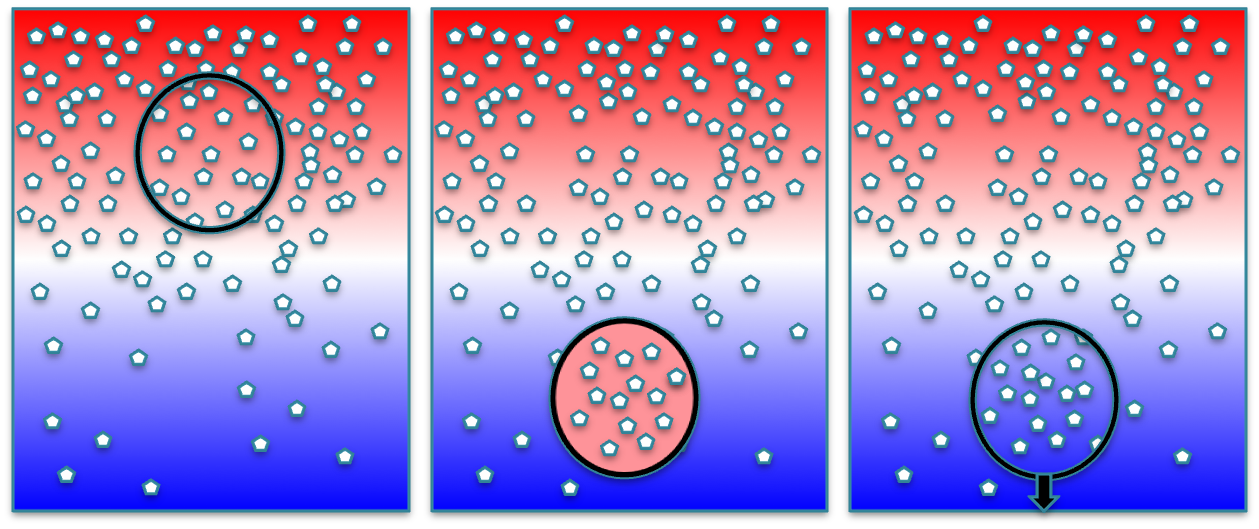
Similar fingering instabilities can occur in any other thermally stably stratified solution, provided the solute concentration increases with height. They are therefore common in astrophysics as well, when by one mechanism or another a stellar radiative zone is subject to an unstable gradient in mean-molecular weight.
The saturated state of the fingering instability, "fingering convection", strongly enhances vertical transport (of heat and composition) in stably stratified regions. It is therefore important to take this effect into account correctly in global dynamical models of a system.
In addition to the small-scale instability itself, fingering convection has a curious propensity to drive the formation of very large-scale structures called "thermo-compositional staircases" (thermohaline staircases in the case of the ocean). These staircases are stacks of very long-lived compositionally and thermally well-mixed convective layers separated by very thin fingering interfaces. Vertical mixing is further enhanced in the presence of thermo-compositional layers.
Upon his arrival in Santa Cruz for a postdoctoral position, Stephan Stellmach developed a high-performance 3D code to study fingering convection (and the related double-diffusive convection). Thanks to this code we have now achieved the following milestones.
In the oceanic context:
- We have calculated numerically the transport properties by small-scale fingering convection in the oceanic heat-salt system. Our small-scale flux laws are in broad agreement with oceanic field measurements. (Traxler, Stellmach, Garaud, Radko & Brummell 2010).
- We have studied numerically the formation of thermohaline staircases, and validated the basic layer-formation theory proposed by Radko (2003), in which a large-scale secondary instability of homogeneous fingering convection leads to the spontaneous growth of horizontally-invariant "staircase-like" perturbations. Furthermore, we have discovered how the interaction of this so-called gamma-instability and the better-known "collective instability" leads to the pre-selection of a particular initial staircase "step" height. (Stellmach, Traxler, Garaud, Brummell & Radko, 2010).
- We have developed a generalized theory for the study of these secondary large-scale instabilities which unify existing work on the subject. This unified theory can be used to predict the existence of large-scale instabilities for all fingering systems, as long as small-scale fluxes for turbulent heat and compositional transport are known as a function of the local stratification. (Traxler, Stellmach, Garaud, Radko & Brummell 2010).
In the astrophysical context:
- We have found simple asymptotic laws describing how the turbulent heat and compositional fluxes scale with the background stratification and the fluid properties. These laws can be applied directly to model transport by fingering convection in a very wide variety of astrophysical systems. (Traxler, Garaud & Stellmach, 2010).
- Using these flux laws in combination with Radko's layer-formation theory, we have established that thermocompositional layers are unlikely to form in stellar environments. (Traxler, Garaud & Stellmach, 2010).
- Using these flux laws, we have established that fingering convection is unlikely to provide sufficient vertical transport to explain the observed surface abundances of RGB stars. (Traxler, Garaud & Stellmach, 2010).
- Using these flux laws, we have also established that the statistically higher metallicity of planet-bearing stars cannot be the result of pollution by infalling planets. Instead, it must be of primordial origin. (Garaud, 2010).
Potential PhD projects:
- (in collaboration with A&A faculty) Application of the fingering flux laws to study the role of fingering convection in AGB stars, and in cataclysmic variables.
- (in collaboration with AMS faculty) Study of the effect of rotation on fingering convection at low Prandtl number.
Understanding the properties of double-diffusive convection, with applications to astrophysics
Collaborators: Nic Brummell (UCSC Applied Mathematics and Statistics), Jonathan Fortney (UCSC Astronomy & Astrophysics), Timour Radko (NPS Monterey), Stephan Stellmach (U. Muenster, Germany)
Funding: NSF AST-0807672
When the density of a fluid depends on (at least) two components, stably-stratified systems can undergo double-diffusive instabilities, leading to strong turbulent mixing. Two cases exist: the "fingering” instability, which often occurs in fluids which are thermally stably stratified, but have an inhomogeneous (destabilizing) composition and the "diffusive" instability, where the fluid is stably stratified despite an unstable thermal gradient.
By contrast with the fingering instability (see previous section), the diffusive instability has an oscillatory nature, and the most unstable modes are similar to "overstable" gravity waves (i.e. gravity waves with an exponentially-growing amplitude). This phenomenon can occur in the ocean for example under ice-shelf, where the slow melting of the ice releases cool fresh water over the warmer, saltier water below.
In astrophysics, it is usually referred to as "semi-convection" and ubiquitously takes place at the edge of convective cores in higher-mass stars. Indeed, nuclear reactions generate high mean molecular weight material, and strong stable compositional gradients develop at the edge of the thermally unstable convective region. It is also thought to regulate heat and compositional transport in giant planets. Indeed, in the core-accretion scenario of planet formation, giant planets are formed by the accretion of a vast amount of hydrogen/helium gas by an Earth-mass size rocky core. The heat released, first by the accretion process and then by the slow gravitational contraction of the planet, drives convection and entrains metal-rich material into the envelope. A strong compositional gradient is therefore created, and normal convection may be suppressed in the vicinity of the core-envelope interface in favor of semi-convection.
Turbulent transport in diffusively-convective regions, as in the case of fingering convection, often controls the structure and dynamics of the entire system. As in the fingering case as well, diffusive convection also leads to the formation of thermohaline staircases in the heat-salt system. Whether such staircases form in the astrophysical semi-convection regime has, by analogy, been postulated, but never established.
Thanks to the code developed by Stephan Stellmach, we have also been able to study the dynamics of diffusive convection and the possibility of layer formation in this context. Our main results, presented in Rosenblum et al. 2011 and Mirouh et al. 2012, are:
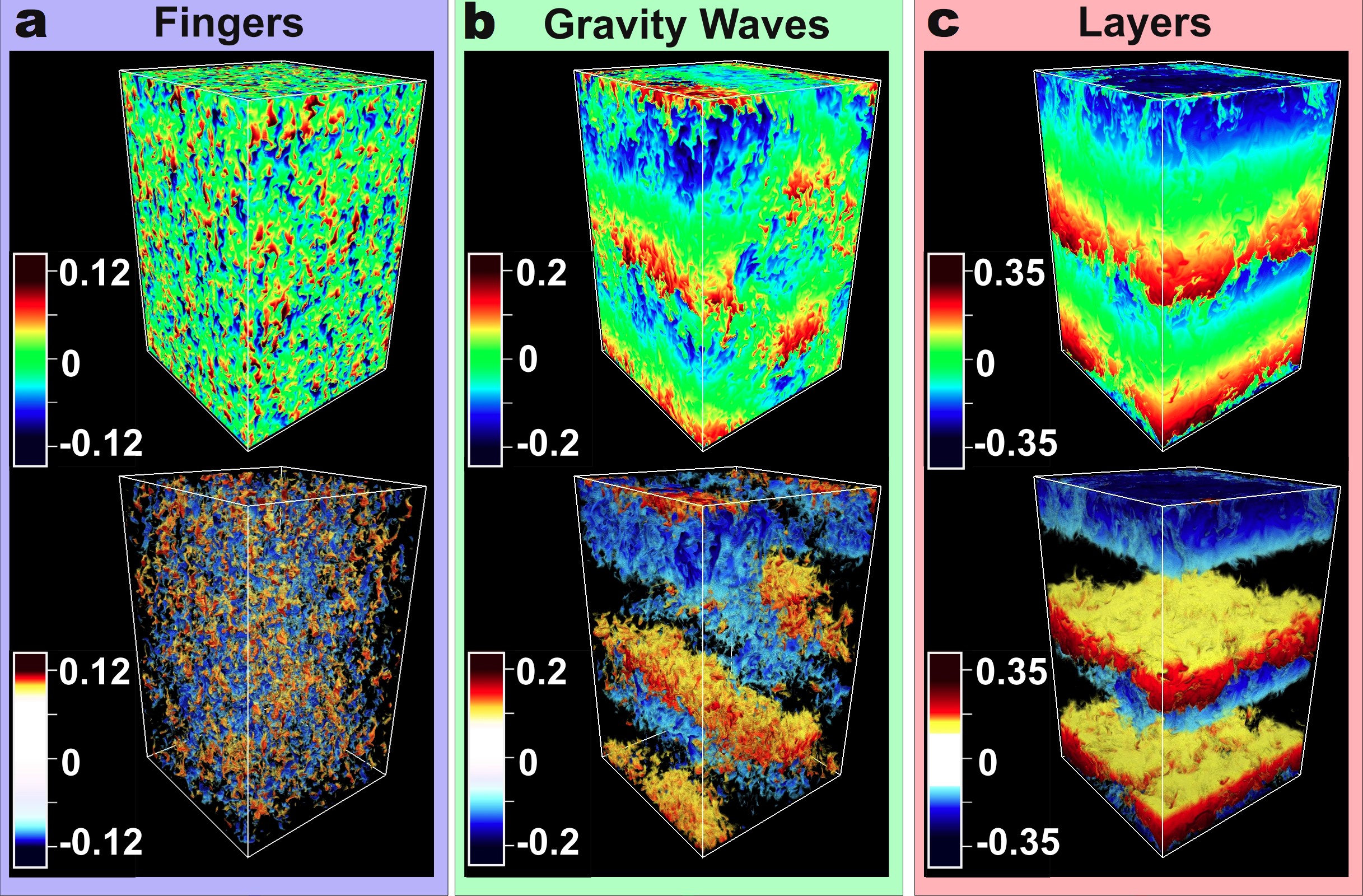
- We find that layers do form, via the same large-scale instability mechanism as in the case of fingering convection. The layers later merge, and each merger is accompanied with a strong increase in the mixing rates. See below for a few snapshots of a semi-convective system undergoing layer formation and mergers.
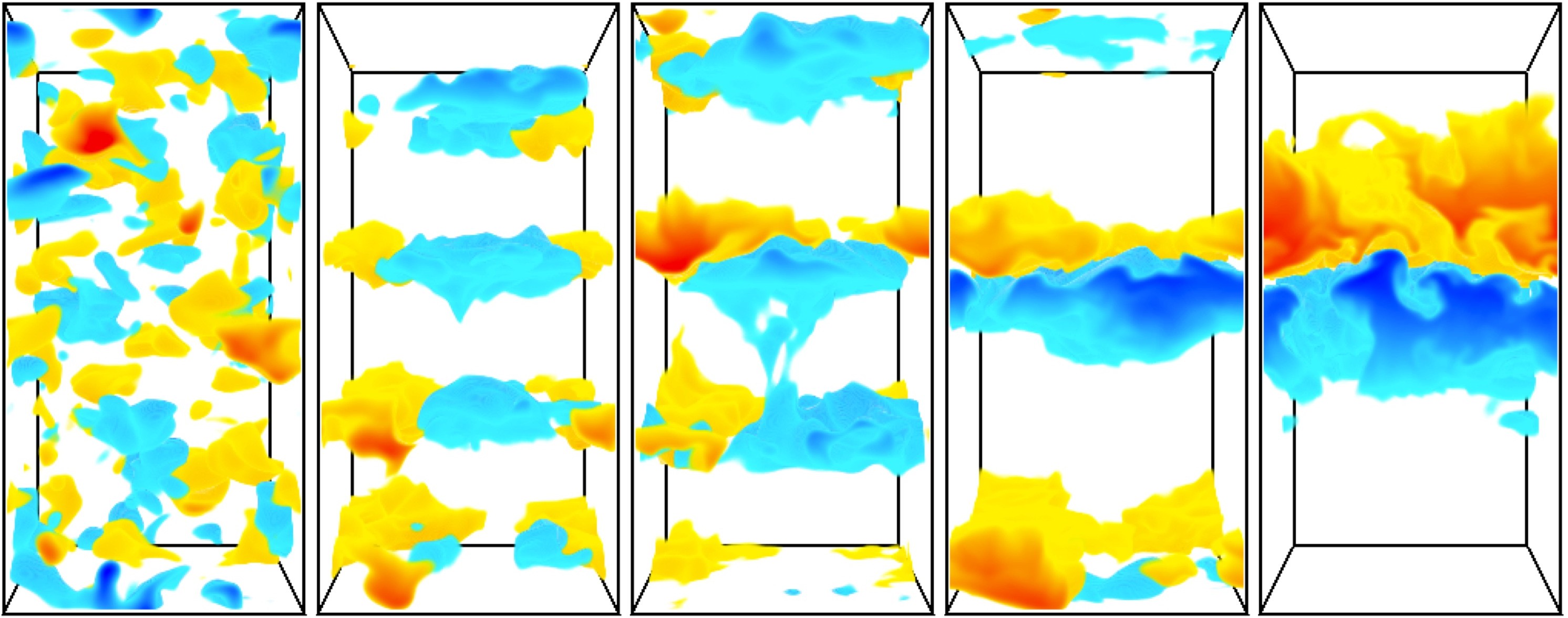
- Whether layers form or not depends on how stronly stratified the system is. More weakly stratified system are more likely to form layers than more strongly stratified ones.
- In the strongly stratified case, turbulent transport by homogeneous double-diffusive convection remains weak
- In the weakly stratified case, turbulent transport by layered double-diffusive convection can be quite significant, and depends sensitively on the depth of the layers.
Potential PhD projects:
- Running systematic numerical experiments to find asymptotic turbulent transport laws similar to the ones obtained in the fingering case.
- (In collaboration with Jonathan Fortney, A&A) To use these transport laws to create between models of planetary structure and study the effect of diffusive convection on the planetary mass-radius relationship.
- To study the layer merger process both numerically and semi-analytically following Radko (2005).
Modeling turbulent convection
Collaborators: Gordon Ogilvie (DAMTP, Cambridge), Stephan Stellmach, (U. Muenster, Germany). Previous students: Neil Miller (UCSC Astronomy & Astrophysics).
Funding: NST MRI-0521566, NSF AST-0607495, NSF CAREER-0847477
Modeling turbulence in astrophysics and geophysics is arguably the most important and yet most complex problem faced by today's generation of scientists. Turbulence is ever present, and controls the large-scale structure and dynamics of all physical systems. Unfortunately, the properties of turbulence are strongly dependent on the presence of forces or large-scale flows, such as buoyancy, self-gravitation, magnetic fields, shear, rotation, etc... As such, a general theory of turbulence remains a far-distant possibility.
In this research project, initiated through a collaboration with Gordon Ogilvie (DAMTP, Cambridge), we focus on a specific case often relevant in astrophysics, where the turbulence is fully-developed and weakly affected by the aforementioned forces and large-scale flows. In this case, a well-defined turbulent cascade develops, and its properties are inherently local.
By extending prior work of Ogilvie (2003) on MHD turbulence, we have developed a second order turbulence closure model for convection, which can be applied in the presence of weak shear and weak rotation (and by extension, weak magnetic fields). The model consists of a set of evolution equations for the Reynolds stress tensor, the turbulent heat flux and the rms temperature, which need to be solved in conjunction with evolution equations for the large-scale temperature and flow profiles.
The model was successfully calibrated against numerical simulations and laboratory experiments of shear-induced turbulence (Garaud & Ogilvie 2005) and turbulent convection (Garaud, Ogilvie, Miller & Stellmach, 2010). On the left are numerical simulations of our collaborator Stephan Stellmach for convection between two plates, and on the right, our model predictions for the variation of the heat flux against the distance from the domain boundary against the results of his experiments.

Potential PhD project: using the turbulence closure model developed, to study the differential rotation observed in stellar convection zones, in particular that of the Sun (see below). Strongly motivated and mathematically savvy student required.
The role of gyroscopic pumping in stellar interiors
Collaborators: Peter Bodenheimer (UCSC Astronomy & Astrophysics), Nic Brummell (UCSC Applied Mathematics and Statistics). Current students: Luis Acevedo-Arreguin (UCSC Applied Mathematics and Statistics).
Funding: NST MRI-0521566, NSF CAREER-0847477
Stars which have outer convective regions often exhibit a significant amount of surface differential rotation, with the equatorial regions rotating faster than the poles. This differential rotation is thought to be maintained by a systematic equatorward transport of angular momentum by anisotropic turbulent stresses (see previous section), which continually accelerate the equatorial regions and decelerate the poles in a manner most remarkably observed in the solar convection zone (see next section for example).
This acceleration of the equatorial regions is a local source of angular-momentum to the fluid, which by angular-momentum conservation must move outward from the rotation axis. Similarly, fluid in the polar
regions must move toward the rotation axis. As illustrated in the figure below (left), the process naturally drives large-scale meridional flows throughout the outer convection region, with an upwelling near the equator, a poleward velocity near the surface and downwelling near the poles. Naturally, a similar mechanism may also operate in an inner convective region of a star.
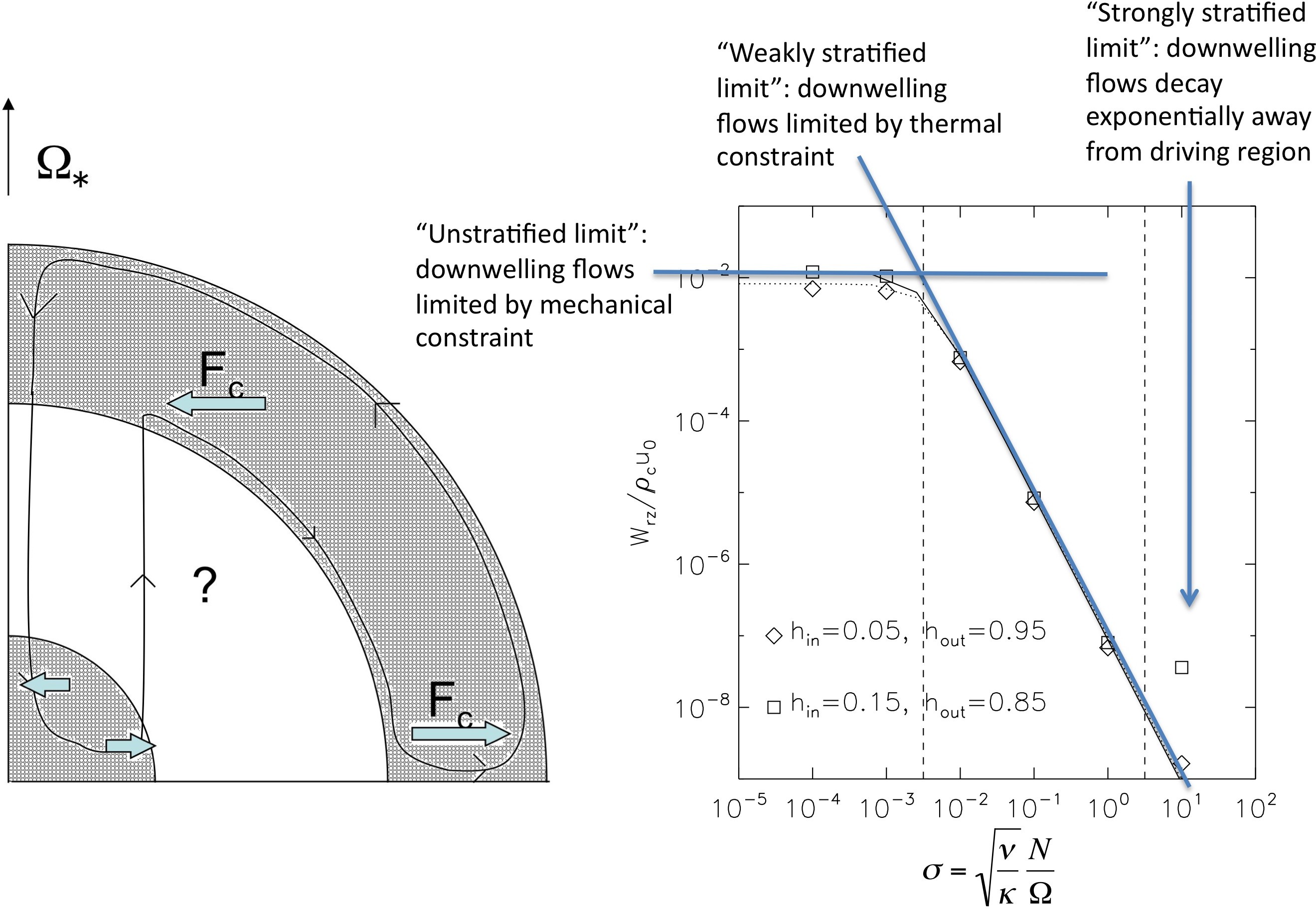
A question of fundamental interest in stellar structure and evolution theory is whether these flows generated in convective regions participate in mixing the nearby stably stratified radiative regions. Over the past 3 years, we have studied the process in detail and found a set of simple rules to answer this question:
- The amplitude of flows generated in a convective region decays exponentially with depth away from that region on a lengthscale R/sigma (where sigma is defined above, nu is viscosity, kappa is thermal diffusivity, N is the buoyancy frequency and omega is the stellar rotation rate). See Garaud & Brummell (2008).
- As a result, if sigma << 1 then the flows may penetrate deeply in the radiative zone. The total mass flux in the direction parallel to the rotation axis is constant (a by-product of the Taylor-Proudman constraint). See Garaud & Bodenheimer (2010).
- In the case sigma << 1, the amplitude with which the flows do enter the radiative zone depends on the radiative zone physics. It is limited by 2 constraints, as illustrated in the figure (right).
- A thermal constraint, which limits the flow amplitude to a local Eddington-Sweet velocity
- A mechanical constraint, which depends on the existence and nature of stresses in the radiative zone to break the Taylor-Proudman constraint. These could be turbulent stresses in another convection zone (as illustrated in the figure, see Garaud & Bodenheimer 2010), or magnetic stresses (see McCaslin, Garaud & Wood, 2011, in prep).
We are currently exploring the implications of our findings for the dynamics of a variety of stars. See the next section for the case of the Sun, for example.
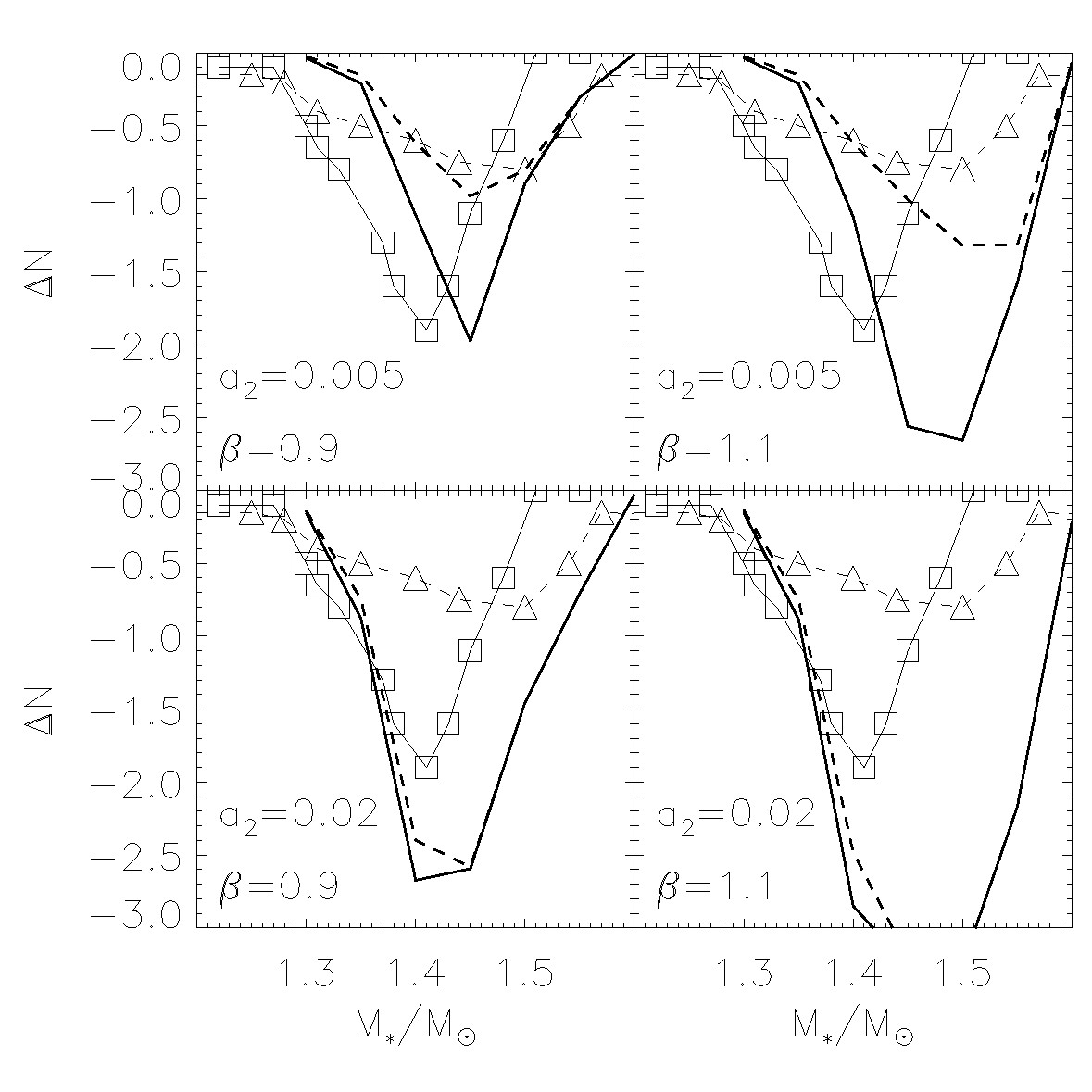
A recent success of the model was to provide a simple explanation for the presence of the well-known Lithium and Beryllium dips in young star clusters such as the Hyades (see Garaud & Bodenheimer 2010 for detail), as shown in the figure below. The figures show the relative Li and Be abundance deficit for stars in the mass range of 1.2-1.6 solar masses, compared with slightly more massive and less massive stars. The thin lines with symbols are observations from Boesgaard (2005), with solid lines for Li and dashed lines for Be. The corresponding thick lines are our own model, for different model parameters (a2 measures the differential rotation of the inner convective region, and beta is related to overshoot).
Potential PhD project: application of gyroscopic pumping to mixing in RGB and AGB stars. Student with experience in stellar evolution models preferred.
Evolution of magnetized stars
Collaborators: Toby Wood (UCSC Applied Mathematics and Statistics). Current Students: None.. looking for students.
Funding: NSF CAREER-0847477
This project is still in very early stages, and aims to combine all of the tools and findings described in the previous 3 sections to create 2D stellar evolution models which include magnetic fields, large-scale flows, and a fairly realistic description of the turbulent angular momentum and heat transport by convection.
This project has multiple phases:
- To implement the turbulence closure model for convection in a spherical coordinate system numerically, and check the behavior of the model against 3D numerical simulations of turbulent convection (see here)
- Once done, to merge the more realistic convective region model with the existing code described in the previous section, and study the dynamical structure of various classes of magnetized, differentially rotating stars
- Study semi-analytically the behavior of the numerical solutions, and extract asymptotic scaling laws for the flow velocities as functions of governing diffusion parameters (viscosity, thermal diffusivity, magnetic diffusivity). This is a crucial step of the project since codes cannot achieve actual stellar values of these diffusion parameters, and rules will have to be obtained to convert "code results"into "observable results". We have proved that this can be done in the non-magnetic case in Garaud & Bodenheimer (2010).
- Once done, combine the structure code with a stellar evolution code to study stellar evolution with more realistic internal dynamics.
Possible PhD projects: all of the above. Strongly motivated and mathematically savvy student required.
Modeling the dynamics of dust particles in proto-stellar disks
Collaborators: Katherine Kretke (SWRI Boulder), Doug Lin (UCSC Astronomy & Astrophysics). Current Students: none.
Funding: unfortunately I have never managed to secure funding for this line of research. Students are advised to apply to work on this topic with their own source of funding.
In the standard paradigm of planet formation, planets are formed within the proto-stellar disks which are ubiquitously observed around young stars. These disks naturally form by conservation of angular momentum, and the gas within the disk is typically cool enough (except very close to the central star) for water and high-metallicity material (principally silicates) to condensate onto small micron-size grains. By repeated random collisions, these grains slowly grow, and are thought to eventually reach large-enough mass for mutual gravitational interactions to become relevant. At this point, the "planetesimals" rapidly grow into planetary-sized objects.
One of the most crucial steps of the process, however, is the growth from mm-size to km-size objects. During that time, the grains also decouple dynamically from the gas, and begin to migrate towards the central star. Unless they grow fast enough, they fall onto the star before they evolve into planets.
In the past 10 years, I have collaborated with Doug Lin on various aspects of the problem, and in particular studied:
- The sedimentation of the grains towards the disk mid-plane, and the role of that sedimentation process in driving shear instabilities in the disk (Garaud, Barriere-Fouchet & Lin 2004, Garaud & Lin 2004)
- How the presence of the grains affect the thermal structure of the disk and its optical properties (Garaud & Lin 2007)
- The growth and migration of the grains in protostellar disks (Garaud, 2007). For this purpose, I developed a method for studying the approximate evolution of a grain population through its size distribution function, and implemented it in a numerical evolution code. The model includes grain growth, migration, sedimentation, and evaporation/condensation. This code was then later used to study...
- The role of the snow line in the formation of planets around intermediate-mass stars (Kretke, Lin, Garaud & Turner, 2009)
Possible PhD projects: to be discussed in collaboration with Doug Lin.
Parallel numerical algorithms for the solution of boundary value problems.
Collaborators: Jean-Didier Garaud (ONERA, Paris, France). Current Students: Luis Acevedo-Arreguin (UCSC Applied Mathematics and Statistics).
Funding: NST MRI-0521566, NSF AST-0607495, NSF CAREER-0847477
As part of the development of the numerical code for our "Evolution of magnetized stars" project, we have developed some "easy-to-use" FORTRAN parallel algorithms for the solution of large systems of block tridiagonal matrices, and of 2-point boundary value Ordinary Differential Equations. The basic algorithms used are described in Garaud & Garaud (2008) (appendix), and the user manuals are available here. Please email me to request the code.
I am currently developing a very similar algorithm for the solution of 2D elliptic problems, which will be used toward the development of 2D stellar structure codes.

