Question of the day: I am given 1000 random integers between 0 and 100. What is the least number of steps it will take you to sort the list of numbers?

House Keeping

• Procedural Literacy
  • http://www.bogost.com/writing/process_intensity_and_social_e.shtml
• Puzzle Solution: http://www.datagenetics.com/blog/july22012/
• Final Projects: http://eldar.mathstat.uoguelph.ca/dashlock/CIG2013/competitions.html
• Blogs!

Review

• Comparing 2 languages: (Processing and Java)
• http://jtf.acm.org/demos/acm.graphics/index.html
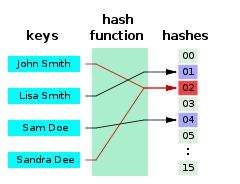
• Hash Tables: terminology
  • int hashed by mod
  • name hashed by sum of letters
  • complex class hashed by big complex equation
• http://www.csanimated.com/browse.php

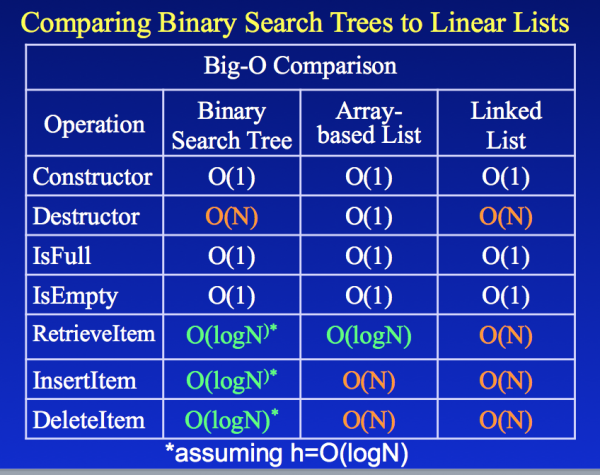
Big O

• Sorting:
  • http://www.sorting-algorithms.com/
  • http://visualsort.appspot.com/

• Merge Sort - recursion!
  • Lisp Merge

Lisp

• Simple Wikipedia
• Normal Wikipedia
• http://classes.soe.ucsc.edu/cmps148/Spring07/micro-talespin.lsp
• http://www.dynamiclearningcenter.com/samples/

More recursion

• http://www.cs.man.ac.uk/~pjj/cs2121/fix.html
• Lisp Arithmetic

(defun merge-sort (list)
  (if (small list) list
    (merge-lists
		(merge-sort (left-half list))
		(merge-sort (right-half list)))))
 
(defun right-half (list)
  (last list (ceiling (/ (length list) 2))))
(defun left-half (list)
  (ldiff list (right-half list)))
 
(defun small (list)
  (or (null list) (null (cdr list))))
 
(defun merge-lists (list1 list2)
  (merge 'list list1 list2 #'<))
 
(print (merge-sort '(2 4 1 2 4 2 3 1)))

Deeper into Datastructs:

• Binary Trees
  • BST
  • Red Black Trees
• Non-Binary Trees
  • 2-3 (B) Trees
  • kD Tree
• Heap
  • Heap Sort
  • Binomial Heap
  • Fibonacci Heap
• Graph Theory

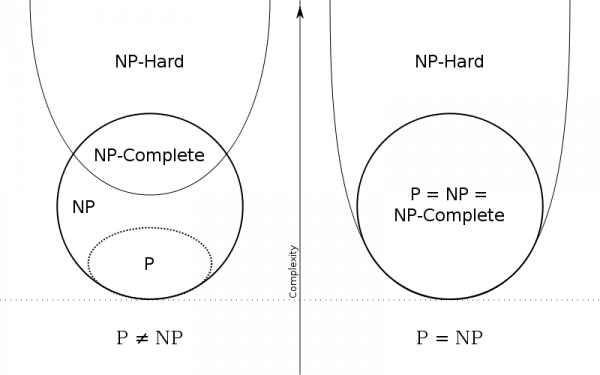
NP-Complete Problems

• http://en.wikipedia.org/wiki/Travelling_salesman_problem

Big O

• O(polynomial degree k) = O(n^k)
• O(1) - constant time
  • query i-th element in array
  • query hashmap
• O(log n)
  • binary search
• O(n) - linear time
  • remove element from array
  • find element in linked list
• O(nlogn) -
  • quicksort
• O(n^2) - quadratic time
  • find closest pair of points
• O(2^n) - exponential time
  • consider all subsets
• Sorting algos, find their Big O (Best, Worst, Average)
  • insertion - B O(n), W O(n^2), A O(n^2)
  • qsort - B O(nlogn), W - O(n^2), A O(nlogn)
  • bogo - B O(n), W = O(inf), A O(n! * n)
• Big O for recursive algos
  • fib O(2^n)
  • memorization → O(n)

• Journal 4
• Assignment 4
• Feedback