Note: this assignment was originally created by David Bernick, then edited by Kevin Karplus. Both are about equally responsible for the final shape of the assignment.
Feature prediction within genomic data is a powerful method for us to learn novel relationships armed with little more than a biological model and a way to express that model in terms of a score. You have seen already that when we can score nature's choices for amino acid substitution, we can use that score as a means to align protein sequences. Similar models can be created to infer phylogeny, ancestral sequences or in searches for sequences that code for RNA structures (e.g., tRNA or snoRNA).
Proteins that bind specific regions of DNA, either as a regulation mechanism (transcription factors), or to recognize foreign DNA (phage DNA) need to make use of short sequences. These sequences need to be short in order to minimize the complexity of the binding protein, and they need to be specific in order to produce a specific regulatory effect. Consider, for example, what would happen if a regulatory protein that targets destruction of viral DNA happened upon that same sequence within the host genome. The benefits to the host of reserving these “special words” can now be seen. Since the machinery that makes use of these “special words” is also quite complex, we would tend to see them preserved over evolutionary time.
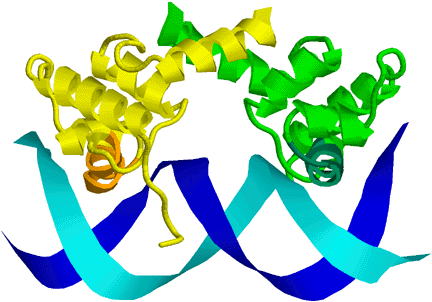
One class of special words appear to be DNA palindromes, which are reverse-complement palindromes (that is, the word is the same on both strands of the DNA—reversing the word and complementing it gives you back the word). For example, “TATA” is one of the more important palindromic sequences, used to signal start of transcription (http://www.pdb.org/pdb/101/motm.do?momID=67. It can be written as: T A A' T', where A' means the reverse complement of A (T), and T' means the reverse complement of T (A). Palindromes are common recognition sites, because many of the DNA-binding proteins bind as dimers or with two copies of the same protein domain, with the two chains having the DNA binding sites facing each other and recognizing corresponding sections on the forward and reverse strands, as can be seen in this cartoon picture of the PDB file 1LMB:

Rocha et al. (http://genome.cshlp.org/content/11/6/946.full doi:10.1101/gr.153101), noticed that palindromes of size 4 and 6 seem to be under-represented in some prokaryotic genomes. They suggest that this may be due to particular structures (restriction or modification systems) that exist in some prokaryotes and some phage (lambda for example). This may be a mechanism for establishing exclusive use or restricting use of these words within a genome.
So, armed with the possibility that there exist special words, and that these words are sometimes palindromes, can we now see if we can find them in our genome of choice?
For us to predict when a word is missing or under-represented, we need to have a model of the frequency with which we would expect a particular word—this will be our null model. We want to find the palindromes that occur significantly less frequently than would be expected.
There are many null models that are possible, and for this assignment we will make use of a Markov model that models extending the central palindrome in both directions. Note: nothing in this null model is restricted to palindromes—we could use this model to look for any under-represented n-mer. The symmetry of extending in both directions from the central (n–2)-mer is particularly elegant for palindromes, but a very similar method can be made by using an order (n–2) Markov model as the null model. Somewhat surprisingly, the calculation for the expected count comes out the same in either model
To compute the probability that an arbitrary n-mer is the word (W)
that we are interested in, we will use 3 components:
the probability that the core (n-2) bases match, and the probabilities
of the first and last bases given that the core matches.
P(W) = P(W1 | W2...Wn-1) *
P(Wn | W2...Wn-1) *
P(W2...Wn-1) .
If we check for the palindrome N times (roughly the length of the genome),
we would expect to see N*P(W) occurrences of W. We can use counts and
maximum-likelihood estimates of the probabilities in our null model to
get an estimation formula:
E(C(W)) = C(W1...Wn-1X)
* C(XW2...Wn)
/ C(XW2...Wn-1X) ,
where E(C(W)) is the expected value for the count of the number of
times W occurs in the genome, and C(Wi...Wj)
is the actual count of the number of times the word
Wi...Wj occurs. The 'X' character on the subwords
is intended to represent "any character". We are counting the number
of words of length n that agree on the first n-1, the second n-1, or
the middle n-2 positions.
In practice, since our genome sequences are very long, we can ignore
edge effects and just use
E(C(W)) = C(W1...Wn-1)
* C(W2...Wn)
/ C(W2...Wn-1) ,
If n=2, we are not counting empty strings
on the bottom, but the number of 2-letter windows in our training data.
(Actually, I counted the number of letters, which is slightly larger.)
Because our model for the count is the sum of N almost independent
observations, each with probability P(W), it can be well modeled as a
binomial distribution, with variance
Var(C(W)) = N* P(W) * (1-P(W))
= E(C(W)) * (1 - E(C(W))/N) ,
and the standard deviation is
sigma(W) = sqrt(E(C(W)) * (1 - E(C(W))/N)) .
Note: because E(C(W)) is much smaller than N, the variance is
approximately the same as the mean.
We can then compute a Z-score for each of our words:
Z(W) = (C(W) – E(C(W))) / sigma(W) .
Using a Z-score is quite reasonable here, because we are expecting a
distribution very close to a normal distribution.
How big a palindrome can we use this method on? As the palindromes get bigger, the expected counts get smaller, and it is harder to tell whether the number is really significantly smaller than expected. Say we want to have 0.01 probability of a false positive. If we check 4^4 (256) palindromes (the number of palindromes of length exactly 8), we would need a p-value < 3.9E-05 to get an E-value < 0.01. According to a normal probability table (http://www.math.unb.ca/~knight/utility/NormTble.htm), we would need a Z-score < -4 for this level of significance. For a zero count to be at least 4 standard deviations below the expected value, we would need for the expected value to be at least 16. For a megabase genome, the expected number of counts for the 4^8 (64k) different 8-mers should be around 16, so 8-long palindromes are about as big as we can go. For longer palindromes, even a count of zero would not mean significant under-representation.
Note that if we wanted to check all 64k 8-mers for under-representation and not just the 256 palindromes, we'd need a probability of 1.5E-07 of a false positive, or a Z-value around -5.1. This would require expected counts of at least 26 on a 1.7 megabase genome.
Part 1: write a short piece of python code that generates all DNA palindromes for a given range of lengths. I found it useful to first write a (recursive) generator function yielding all k-mers over a given alphabet for a fixed value of k. I also found the following function useful:
# define reverse complement
complement_table = string.maketrans("ACGT", "TGCA")
def reverse_comp(dna):
"""return a string with the reverse-complement of the DNA string "dna".
Assumes that all bases in DNA are canonical (ACGT).
To generalize to wildcard bases, complement_table would need
to be redefined.
"""
return dna[::-1].translate(complement_table)
The definition of DNA palindrome above does not allow odd-length
palindromes, since the middle letter is never the complement of itself.
In practice there are often unimportant bases in the middle of a
matching sequence, so let's add "odd palindromes" that have an extra
letter in the middle: dna+'A'+reverse_comp(dna),
dna+'G'+reverse_comp(dna), ...
Part 2:
Write a program, named score_palindromes, that reports significantly under- or over-represented palindromes. The program should have at least the following options:
Your program would then be executed as follows (for example):
search_nmer -e 0.01 --max_k=8 P.abyssi.fa.gz P.furiosus.fa.gz P.horikoshii.fa.ga
Note: you can open a gzipped file in python fairly
easily using the gzip module.
file = gzip.GzipFile(filename,'r') if filename.endswith(".gz")
else open(filename,'r')
I will provide a few genomes for various prokaryotes as FASTA
files (actually, as gzipped fasta files).
A.fulgidus.fa.gz
A.pernix.fa.gz
H.influenzae.fa.gz
H.pylori.fa.gz
M.jannaschii.fa.gz
M.thermoautotrophicus.fa.gz
N.meningitidus.fa.gz
P.abyssi.fa.gz
P.furiosus.fa.gz
P.horikoshii.fa.gz
S.acidocaldarius.fa.gz
S.solfataricus.fa.gz
S.tokadaii.fa.gz
V.cholerae.I.fa.gz
V.cholerae.II.fa.gz
V.fischeri.I.fa.gz
V.fischeri.II.fa.gz
V.parahaemolyticus.I.fa.gz
V.parahaemolyticus.II.fa.gz
V.vulnificus.I.fa.gz
V.vulnificus.II.fa.gz
These genomes are also available directly from /soe/classes/bme205/Fall05/ on the School of Engineering computers, and it is fairly simple to find other full prokaryotic genomes on the web. There will be one sequence per file, but your program should be able to handle multiple sequences in one file, so that it can be applied to multi-chromosome genomes or genomes that are not fully assembled. You could also apply the program to a set of genomes from the same genus, as the extra data would allow you to search for slightly longer palindromes. Note: the files take up about 45 Mbytes unzipped, so leave them in the compressed format. It is good practice to learn how to read gzipped files without having to uncompress them first, so that is a requirement for this assignment.
Hint: the program could use the k-mer counting module that you developed for the Markov chain assignment, modified to count all k-mers up to the maximum size specified. You can use a single dictionary to store all the different counts, since the k-mer keys are distinct. Note that your previous k-mer counting only counted one strand of the DNA. There is no need to run though the entire reverse-complement strand, as you can get the counts for the opposite strand fairly simply:
rev_counts = dict( (reverse_comp(dna),cnt) for dna,cnt in counts.items())
for dna, cnt in rev_counts.items():
counts[dna] += cnt
After you have counted all the k-mers, you can iterate over all the palindromes that you generated for part 1 and compare the observed counts with computed counts.
It is easy to compute the z-scores, since we have a model for both the mean and standard deviation that we expect. To turn the z-scores into p-values, we need the cumulative normal distribution function. This is not built into Python, but we have access to the math library, which includes the erf() and erfc() functions:
from math import erf, erfc
Use the erfc function to compute the desired p-value. For example, if
you have a threshold t, then the probability of getting a z-value
larger than t is
P(z > t) = erfc(t/sqrt(2))/2
and the probability of getting a z-value less than t is
P(z < t) = erfc(-t/sqrt(2))/2
After we've computed the z-value for a particular palindrome, we can
compute its p-value (the probability of seeing a z-value more extreme
than it).
When I run the command
score_palindromes --max_e=0.01 --min_k=6 --max_k=6 ~/.html/bme205/f05/H.influenzae.fa.gzI get
# Reading from /cse/faculty/karplus/.html/bme205/f05/H.influenzae.fa.gz # Reading from H.influenzae.fa.gz # There are 64 palindromes being considered, # and about 3660050 positions where palindromes could be. # Reporting palindromes from length 6 to 6 , # which are under- or over-represented with E_value < 0.01 #kmer observed expected Z_score E_value GTTAAC 38 673.62 -24.49 5.716e-131 GAATTC 604 1337.26 -20.06 5.812e-88 TAATTA 1832 2820.60 -18.62 6.870e-76 GATATC 352 897.61 -18.21 1.295e-72 GTGCAC 282 760.93 -17.36 4.972e-66 AAGCTT 718 1302.25 -16.19 1.804e-57 ATGCAT 510 955.62 -14.42 1.292e-45 GGCGCC 54 279.78 -13.50 5.084e-40 GTCGAC 8 186.88 -13.09 1.274e-37 CATATG 348 674.85 -12.58 8.387e-35 CTTAAG 244 517.74 -12.03 7.780e-32 TGCGCA 700 1092.76 -11.88 4.640e-31 AAATTT 5808 6760.86 -11.60 1.330e-29 CAATTG 1348 1840.40 -11.48 5.269e-29 AATATT 4070 4819.54 -10.80 1.056e-25 TTCGAA 352 604.80 -10.28 2.770e-23 GGTACC 144 323.15 -9.97 6.845e-22 CGATCG 284 505.93 -9.87 1.844e-21 TTTAAA 4568 5171.36 -8.40 1.476e-15 ATATAT 850 1131.41 -8.37 1.883e-15 AGCGCT 94 211.23 -8.07 2.322e-14 GCTAGC 122 241.76 -7.70 4.274e-13 GTATAC 114 229.59 -7.63 7.583e-13 GAGCTC 128 243.79 -7.42 3.860e-12 GGATCC 192 323.87 -7.33 7.482e-12 GGGCCC 50 133.22 -7.21 1.791e-11 CAGCTG 620 822.28 -7.05 5.527e-11 CACGTG 472 636.72 -6.53 2.126e-09 CGTACG 234 357.26 -6.52 2.226e-09 GACGTC 70 146.63 -6.33 7.933e-09 ATCGAT 774 961.08 -6.04 5.071e-08 TTATAA 1776 2029.53 -5.63 5.793e-07 CTATAG 204 285.75 -4.84 4.238e-05 TGATCA 978 1138.01 -4.74 6.710e-05 TTGCAA 2518 2740.44 -4.25 6.817e-04 TGTACA 554 651.77 -3.83 4.099e-03 AACGTT 1694 1849.17 -3.61 9.825e-03
BUG: I've not defined a unique output format, so comparison of results will be difficult to do with standard programs like "diff". It will help me if the output is done as 5 columns separated by white space, in the order kmer, observed count, expected count, Z-score, and E-value, and if any other information is done as a comment line that starts with a "#". I can then write a special-purpose comparator program that compares two such files.
If you sort your output by length of word and alphabetically within that, you may see helpful patterns, such as palindromic sequences that have a don't-care region in the center. (My report did not do that sorting, but sorted by Z-score.)
Part 3: Run your program as in the example above (H. influenzae for palindromes of length exactly 6). Also run your program for the three pyrococcus genomes taken together, for length 4 to 8 palindromes:
score_palindromes --min_k=4 --max_k=8 --max_e=0.01 P.abyssi.fa.gz P.furiosus.fa.gz P.horikoshii.fa.gzI'm curious also how long your program takes to run. My unoptimized program took about 104 seconds on an old 32-bit linux box, and 37 seconds on my MacBook Pro (3.06GHz Intel Core 2 Duo).
Write up a short discussion that includes your data, along with an interpretation of their meaning. Is there anything special about these sequences? Try Google, or the following links: http://www.neb.com/nebecomm/tech_reference/restriction_enzymes/cross_index_recognition_sequences.asp and http://rebase.neb.com/rebase/rebadvsearch.html The first page has table, the second has a search site for finding known restriction enzymes by organism or sequence (among other methods). (Use 'N' for wildcard, not 'X' on this search page.) Do your finds match up with known restriction enzymes?
--all) for looking at all n-mers,
and not just palindromic ones—make sure you change the number of
hypotheses when computing the E-values!
One student earned an A this year, by observing and fixing a mistake that I had made. The odd palindromes come in pairs and each pair should be treated as a single hypothesis.
Something I observed, but have not fixed yet in my code, is that the number of positions should be the single-stranded genome length, and the number of occurences of each palindrome should be the number of occurences in the single-stranded genome (so both observed and expected counts are doubled in the current computation). For odd palindromes, the count and reverse count added together are the number of occurences, so they should not be halved, the way the even palindrome counts should be.
The number of hypotheses is really twice what I used here, as the hypotheses "α is under-represented" and "α is over-represented" are separate hypotheses. As a sanity check, the E-value for count=expected_count (Z-score=0) should be the number of palindromes, since every palindrome is at least that extreme.
|
|
| BME 205 home page | UCSC Bioinformatics research |
Questions about page content should be directed to
Kevin Karplus
Biomolecular Engineering
University of California, Santa Cruz
Santa Cruz, CA 95064
USA
karplus@soe.ucsc.edu
1-831-459-4250
318 Physical Sciences Building