Homework 2 (Due 6 pm, Friday, 10/20/2017)¶
Please submit your homework to your git repo by 6 pm, Friday, 10/20/2017.
In this homework, you don’t need to submit Problem 1 but only Problem 2 and Problem 3 by the due date. Although Problem 1 is not required for submission, you’re strongly encouraged to do it for your own educational interests. The Fortran part of Problem 1 will not be graded, but note that there is a bonus problem for creating a shell script.
You’re going to solve all 16 exercise problems in Part 1 of the Prof. Garaud’s notes on Fortran. For Problem 1, you don’t need to check in your solutions to your git repo, but you are still welcome to check them in (recommended). If this is the case, please do the following:
- Make a directory called hw2 and make 16 subdirectories (e.g.,
exercise01, ..., exercise16) under hw2.
- NOTE: Too many subdirectories to generate by hand? You may want to come up with a smart way of generating N many of them (directories, files, etc.) by writing a short shell script on your own. This is definately worth a try, and there will be some bonus points if you implement a short shell script to do this task.
- Include the corresponding Fortran routines in each exercise** directory.
- In each problem please write a short note on your answers, findings and any issues you encounter.
- In all problems, you are going to use double precisions for all real variables. Please do this by using the proper gfortran compilers as we discussed in the class. Indicate what flag options you used.
- Make a directory called hw2 and make 16 subdirectories (e.g.,
exercise01, ..., exercise16) under hw2.
Write a Fortran 90 program(s) to approximate
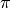 using the sum of the series
using the sum of the series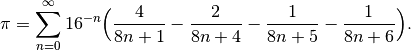
Since you can only add up to a finite number of terms in a practical run, say, summing up to the N th term, you are going to need a stopping criterion on N to obtain an accurate enough numerical approximation. For instance, you can stop the summation if the absolute value of the difference between your approximation
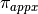 and the reference (or true) solution of
and the reference (or true) solution of 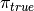 defined as
defined as
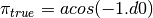 becomes smaller than a threshold value, e.g.:
becomes smaller than a threshold value, e.g.:threshold = 1.e-8 diff = abs(pi_appx - pi_true) if diff > threshold continue summing up else break end
Please report numbers of terms N and the difference diff for four different values of threshold, 1.e-4, 1.e-8, 1.e-12, and 1.e-16. Please make sure you use double precisions for all real variables in your implementation using a proper Fortran flag(s).
Note that you also need to provide a clear instruction on how to compile your code(s), including compilation command(s), compiler flag(s), etc. so that your code result can be reproducible by TA and the intructor.
Write a Fortran 90 algorithm for approximating integral quantities using the trapezoidal rule. For those who are not familiar with the trapezoidal approximation, study the numerical algorithm in the above Wikipedia link. In your code, the main driver routine will call the trapezoidal approximation implemented in two different forms and an exact calculation:
- function implementation,
- subroutine implementation,
- exact implementation,
all of which are in a Fortran module.
For example, a pseudo-code may look like:
function f(x) ... (implement the specific form of your funciton f(x) = x^2 + 1) ... end function function blablah... ... (you may want another function implementation for exact integration...) ... end ! module trapezoidApprox includes two implementations, ! one in function and the other one in subroutine module trapezoidApprox contains ! -------------------------! ! [1] FUNCTION ! ! -------------------------! function trapezoidFunc(...) ... (your function implementation here) ... end function trapezoidFunc ! -------------------------! ! [2] SUBROUTINE ! ! -------------------------! subroutine trapezoidSub(...) ... (your subroutine implementation here) ... end subroutine trapezoidSub ! -------------------------! ! [3] EXACT ! ! -------------------------! subroutine trapezoidExact(...) ... (your subroutine implementation here, assuming that you know the function to integrate and its exact integral value) ... end subroutine trapezoidExact end module trapezoidApprox ! -------------------------! ! Driver routine ! ! -------------------------! program compute_integration ... (this is your driver routine that calls [1] trapezoidFunc, [2] trapezoidSub, [3] trapezoidExact.) ... print*, "[1] Trapezoidal in function =", trapezoidFunc result print*, "[2] Trapezoidal in subroutine =", trapezoidSub result print*, "[3] Exact integration =", trapezoidExact result print*, "[4] Error in function =", trapezoidExact - trapezoidFunc result print*, "[5] Error in subroutine =", trapezoidExact - trapezoidSub result end program compute_integrationTest your code using a function
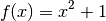
to approximate its integration over
![[a,b]=[0,1]](../../_images/math/61c499074da8048da4f4796f60c71304eaf028b9.png)
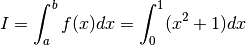
Your input and output are:
INPUT: the endpoints
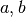 of the interval and the
number
of the interval and the
number 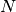 of subintervals
of subintervals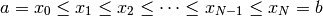
OUTPUT: approximate values from your function, subroutine, and exact implementations.
Make sure you use proper sets of Fortran 90 flags for double precision handlings of floating point operations. It is strongly recommended to test your code using valuable debugging flags too.
Test your code using
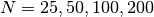 and
and 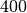 ,
and observe how the errors change as a function of different values of
,
and observe how the errors change as a function of different values of 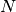 .
.
