[7] Numerical Approximations: Euler’s Method¶
In this section, we learn how to solve DEs computationally, or in other words, by writing a computer code to solve DEs numerically.
Many practical applications using mathematical modelings with DEs (ODEs and PDEs) often do not have analytical solutions. This means that we do not know how to solve those problems in practice.
The methods and examples we learned so far are indeed only a fractional part of DEs in which simple analytical ways are available to solve them.
When analytical theories/methods are not avialble, we then need to rely on computer models to study such general, and more challenging DEs.
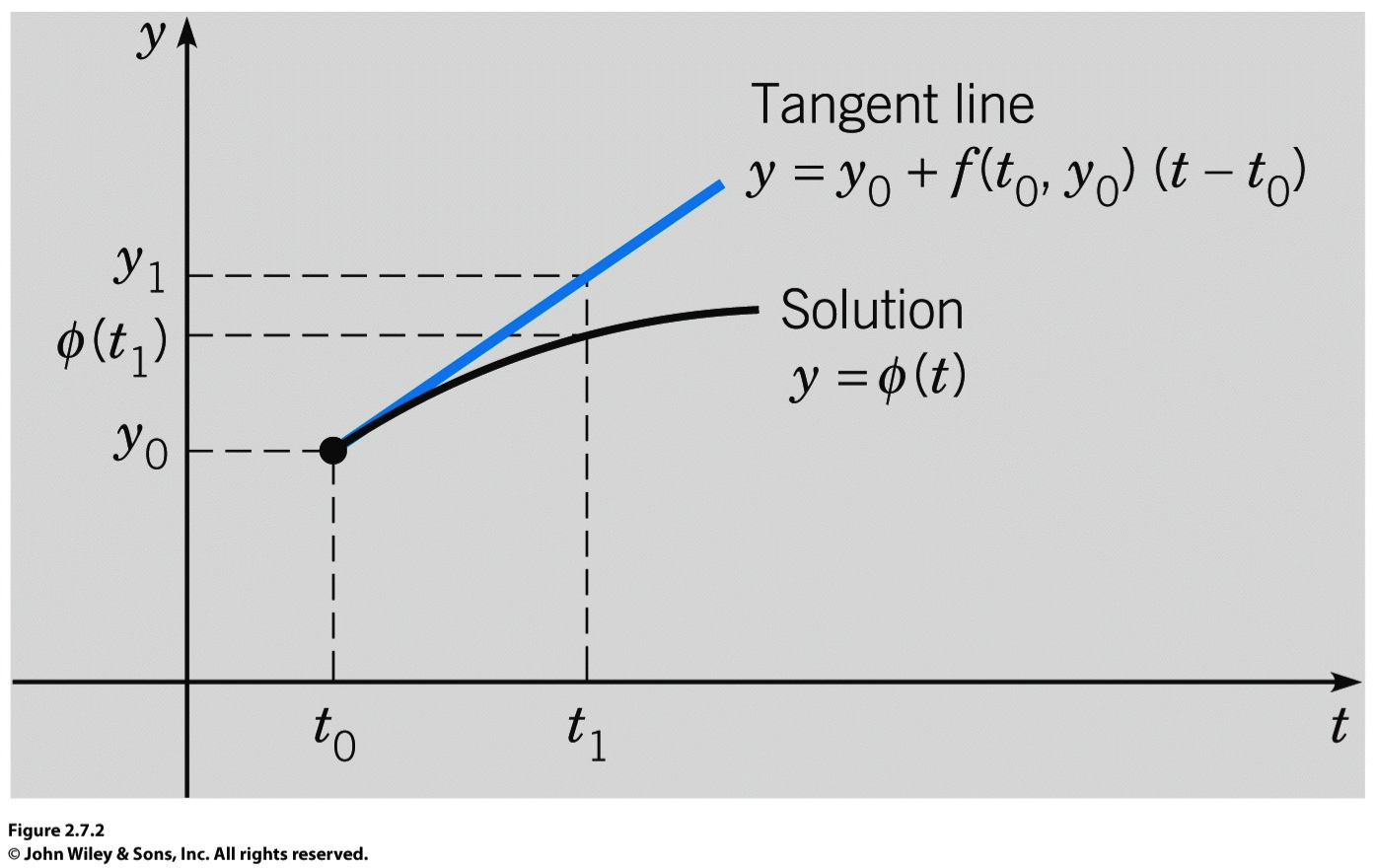
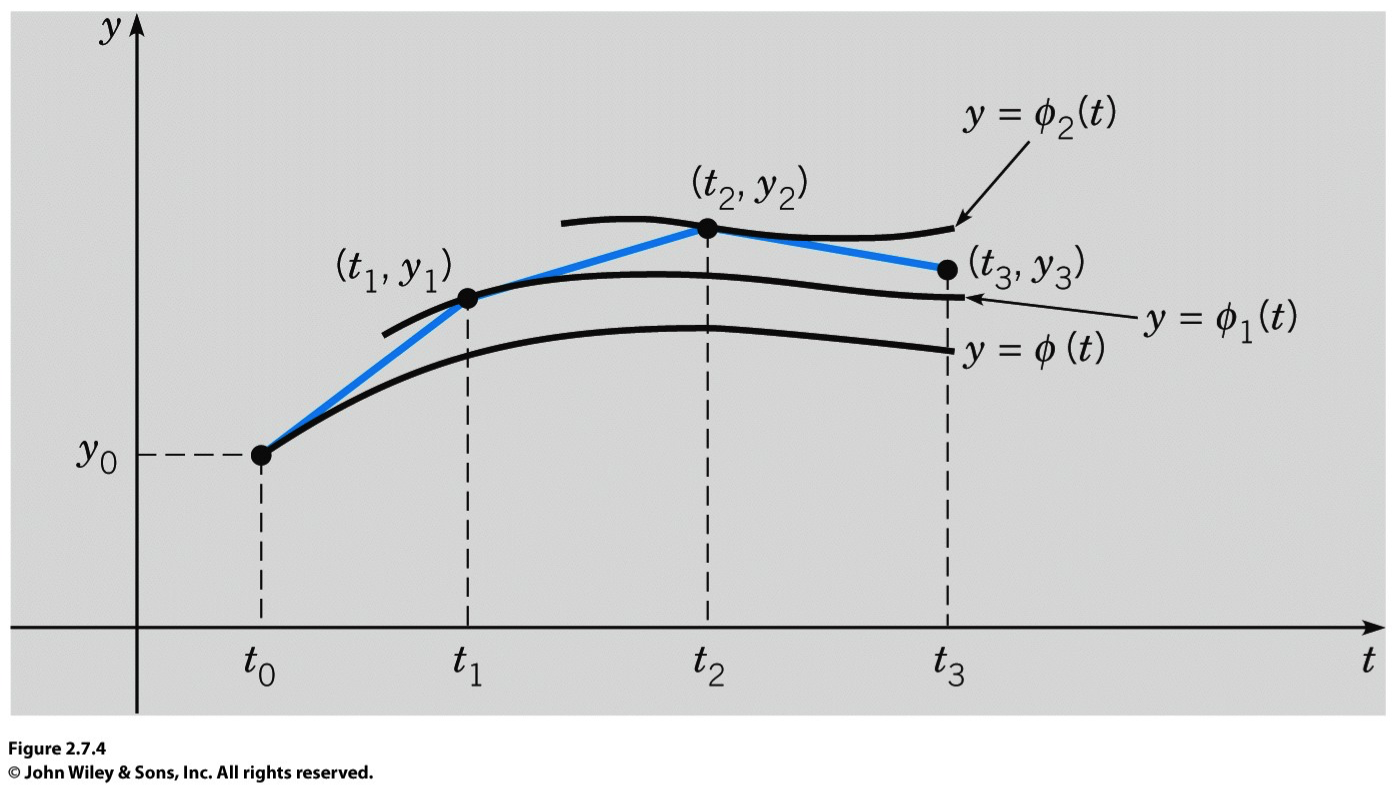
One easy way, due to Euler in about 1768, is based on using tangent lines of the DEs, and the method is called the Euler method (or the tangent line method). To be precise, the method we are going to learn is called the Forward Euler Method in order to represent the discrete approximation of the method is forward in time. That is to say, by considering the definition of derivatives, we see that, for
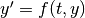 ,
,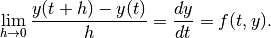
If we choose
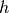 very small then we have
very small then we have(1)
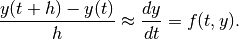
This is called the forward differencing approximation of
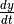 , whereas the backward differencing
approximation can be similarly written as
, whereas the backward differencing
approximation can be similarly written as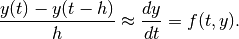
The (forward) Euler’s Method for ODEs
Given the IVP:
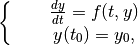
The Euler method takes the following steps:
Choose the initial point
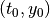 of the IVP.
of the IVP.Introduce a discrete notation
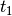 to write
to write
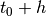 , and in general,
, and in general,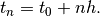
Introduce another discrete notation
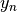 to write
to write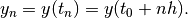
Then Eq. (1) can be written as a discrete difference equation:
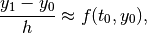
or, equivalently,
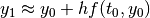
Assume
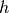 is chosen very small enough so that we
approximately write
is chosen very small enough so that we
approximately write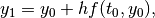
and in the similar way, we successively obtain the
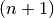 th
term,
th
term,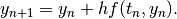
Examples 1 and 2:¶
Solve the IVP
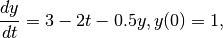
using the Forward Euler method.
Note that using the integrating factor 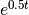 we can obtain
the exact solution
we can obtain
the exact solution
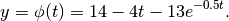
An example Matlab code: Click to download the sample code ForwardEuler.m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 | % --------------------------------------------%
% The Forward Euler Method for ODEs %
% Written by Prof. Dongwook Lee %
% AMS 20/20A %
% --------------------------------------------%
% ---------------------------------------------%
% Example 1: %
% * dy/dt = f(t,y) = 3 - 2t - 0.5y %
% * y(0) = 1 %
% ---------------------------------------------%
% [0] clear any previously defined values and
% figures
clear all;
clf;
% [1] Set initial condition ====================
y0 = 1;
% [2] Set h ====================================
h = .25;
% [3] Set f(t,y) ===============================
f = inline('3 - 2*t - 0.5*y','t','y');
% [3] Temporal Evolution of ODE ================
% [3a] Set your clock to be zero initially
t = 0;
% [3b] Set your maximum timestep
n_step = 100;
% [3c] Set your maximum time based on the
% maximum timestep
t_max = 10;
n_max = 1000000;
% [3b] Temporal evolution of ODE until t=t_max
% Set your current y value y_n to be
% the initial value to begin with
y = y0;
% Provide 1D arrays for solutions of length n_step
y_soln = zeros(n_step,1);
t_soln = zeros(n_step,1);
n = 1;
y_soln(n) = y0;
while (t<=t_max) & (n <= n_max);
%for n=1:n_max;
% Forward difference approximation
y_new = y + h * f(t,y);
% Update your clock
t = t + h;
n = n + 1;
% Update your current value of y
y = y_new;
% Store your time and new solutions
% in arrays for plot
y_soln(n) = y;
t_soln(n) = t;
%end
end
% [4] Plot your numerical solution =============
figure(1)
plot(t_soln(1:n), y_soln(1:n), 'r*')
% [5] Exact solution
y_exact = inline('14 - 4*t - 13*exp(-0.5*t)','t');
% [6] Overplot exact solution
hold on;
plot(t_soln(1:n), y_exact(t_soln(1:n)),'b');
grid on;
|
Questions
Study and understand the code, and run it.
Modify the time step size
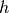 by increasing or decreasing
within the stability range of
by increasing or decreasing
within the stability range of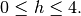
What happens when you increase/decrease your timestep
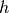 ?
?Modify the time step size
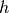 by increasing more than the stability
range so that
by increasing more than the stability
range so that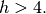
What happens when your timestep
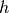 is bigger than the
stability limit 4?
is bigger than the
stability limit 4?The current code implements to exit the temporal evolution based on the maximum timestep, e.g.,
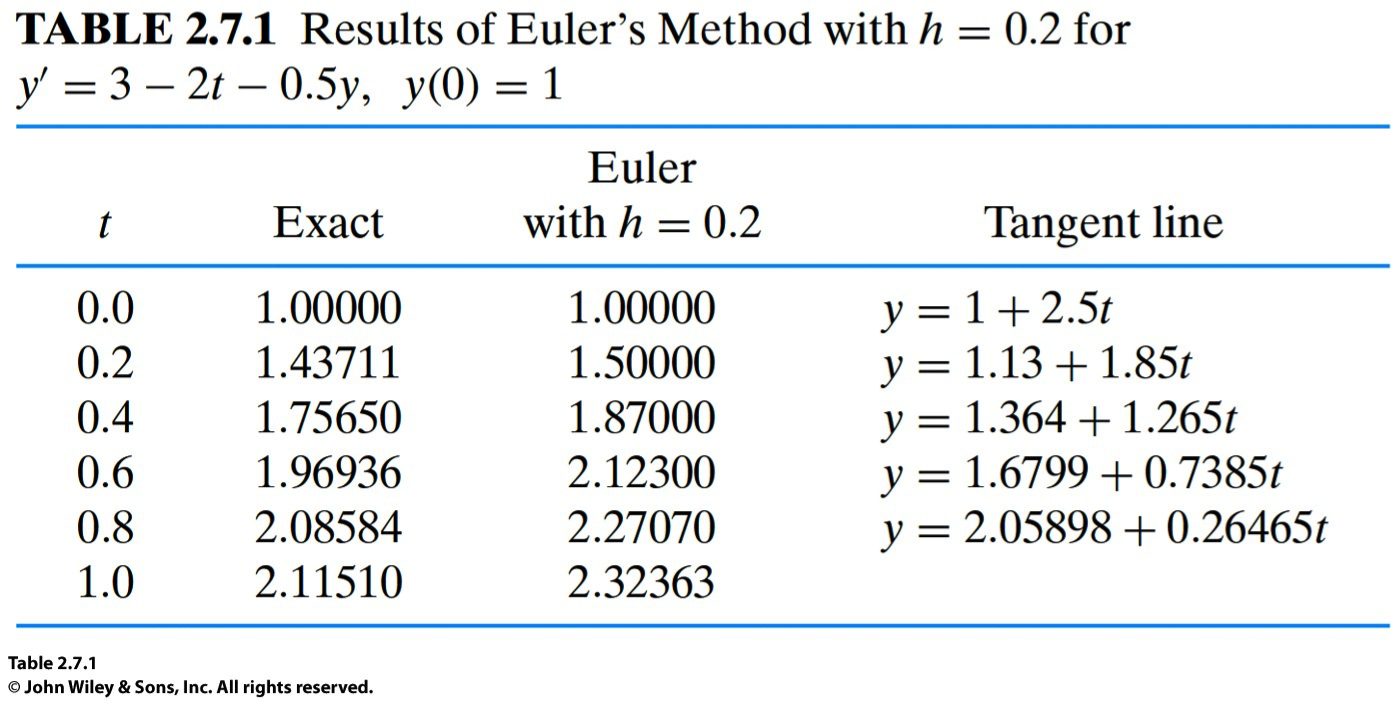
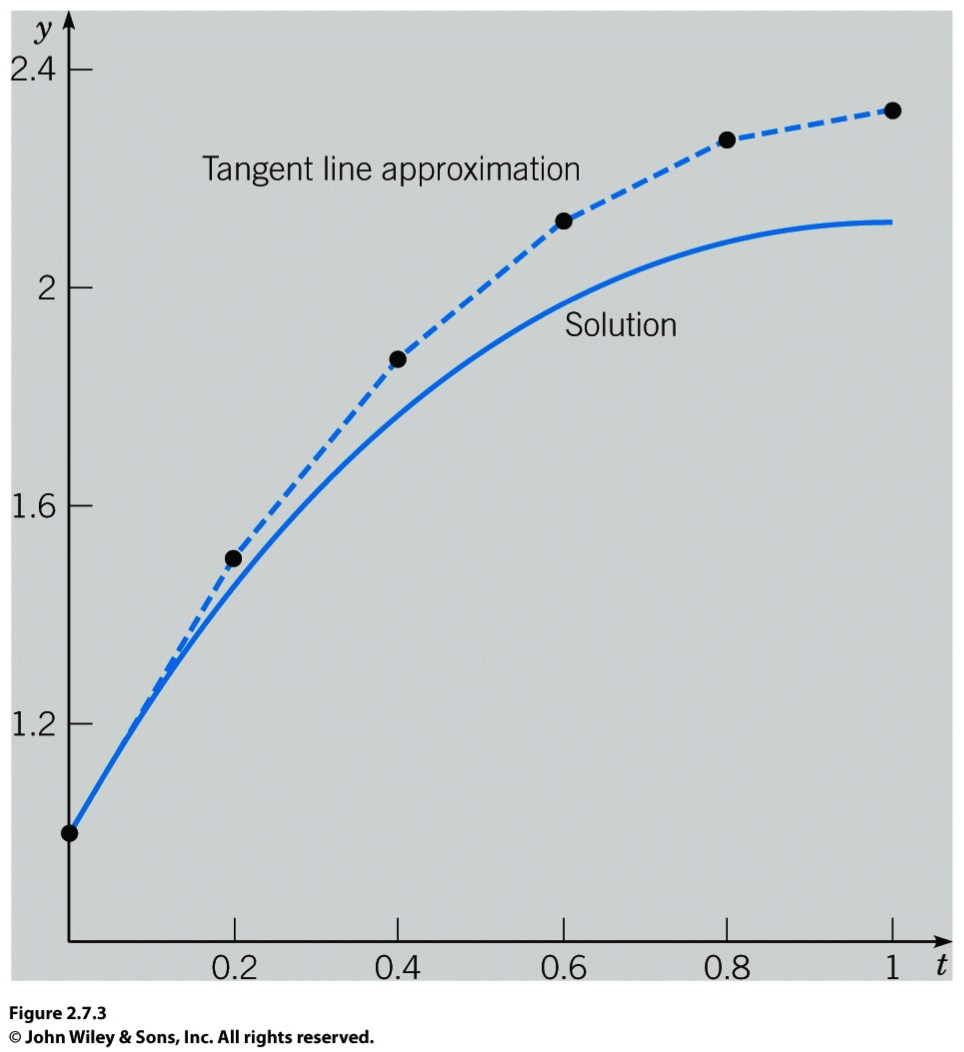
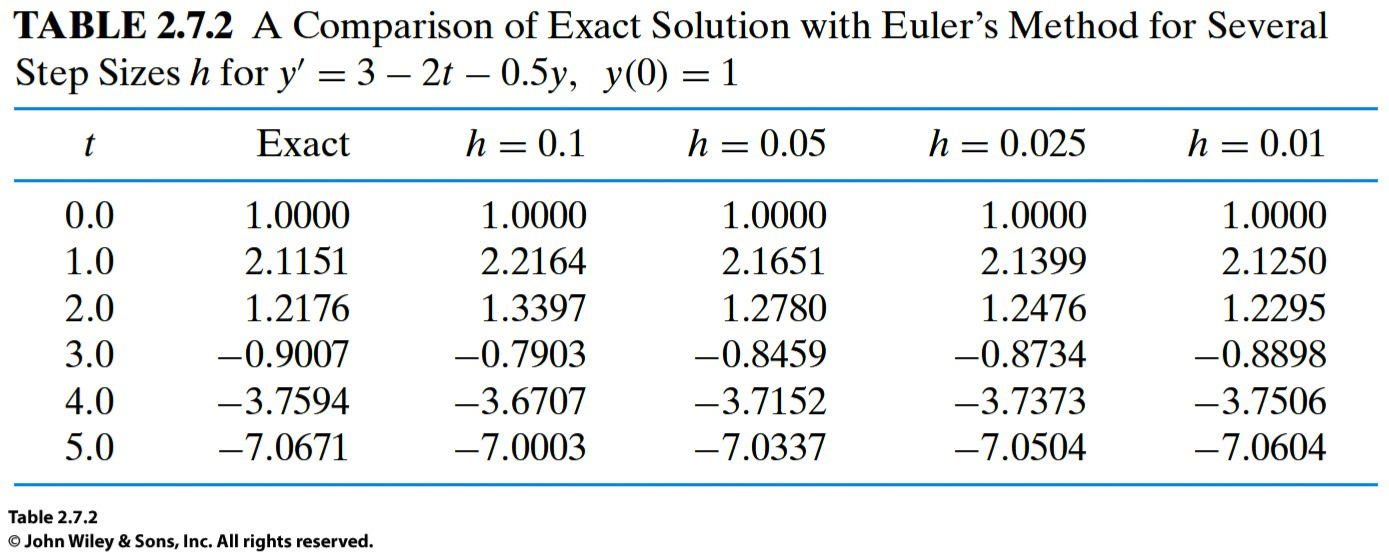
n_step. Modify the exit condition so that the code stops whent=t_max, wheret_maxis any arbitrary time which is not necessarily a multiple ofn_stepas in the current implementation. (hint: usewhileloop instead of usingforloop.)Check if you can reproduce the numbers in Table 2.7.1 and Table 2.7.2.
Note
We do not learn how to obtain a stability limit for timestep
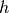 in this class. Such topics are covered in
more advanced numerical ODE/PDE classes
(e.g., AMS 213B).
in this class. Such topics are covered in
more advanced numerical ODE/PDE classes
(e.g., AMS 213B).For this problem, as long as you keep the time step size
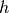 to satisfy the stability bound,
to satisfy the stability bound,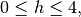
the numerical solutions of the Forward Euler method are stable.
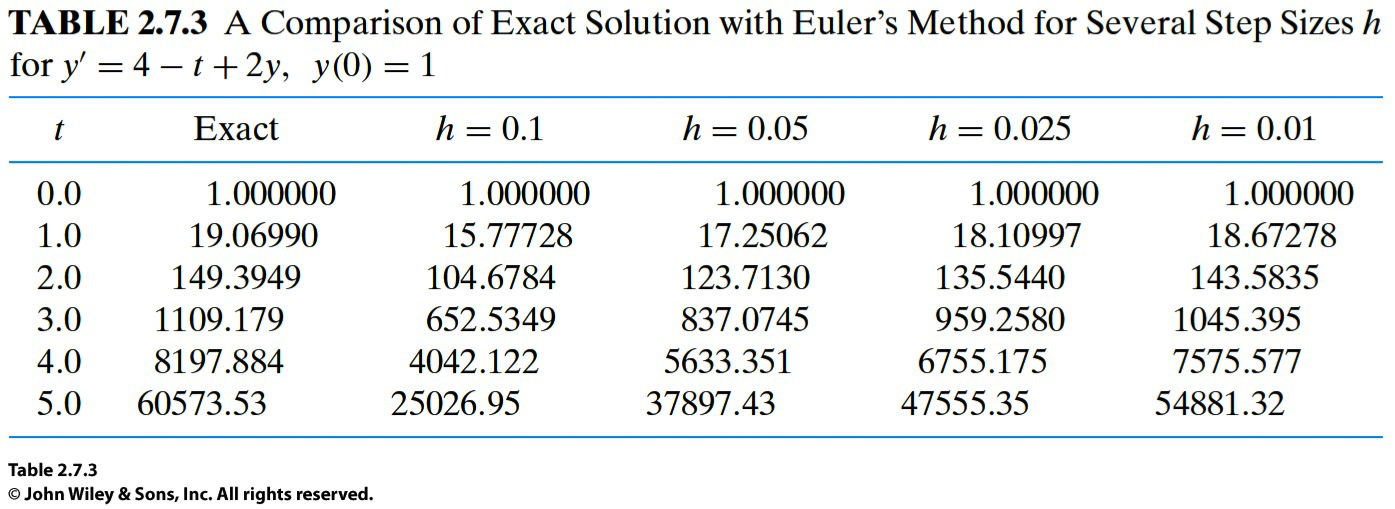
Example 3:¶
Solve the IVP
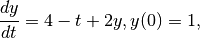
using the forward Euler method.
Questions
- Find the exact solution.
- Modify the code in Examples 1 and 2 to solve this problem.
- Repeat the steps in Example 1 and 2 and see if the solutions
converge by visually inspecting the departure between the numerical
and exact solutions, in particular, for large
 .
.
Note
For this problem, the mathematical stability bound of the time step size
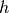 becomes
becomes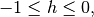
which implies the Forward Euler method always fails to be stable, no matter how
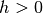 is small, for the
given ODE.
is small, for the
given ODE.The unstably divergent solution behaviors are shown in Table 2.7.3, in which the differences between the exact and numerical values at times
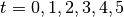 are much bigger than
Examples 1 and 2, for all choices of
are much bigger than
Examples 1 and 2, for all choices of 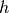 .
.In this situation, one has to use a different numerical method, such as the backward Euler method (harder than using the forward Euler method in general), in order to stably solve the problem numerically.